Example: An object with mass m = 3.2 kg sits on an incline plane at an angle θ = 23°. The object slides down the incline with s = 1.9 m, starting from rest. Find the speed of the ball at the end of the ramp.
Solution: The net force on the object is equal to the component of weight parallel to the incline, Fnet = -mg sin θ ; here the negative sign implies that the force is directed downward. We thus get for the work:
W = Fnet s= mg sin θ • s = mgh,
where we use s sin θ = 1.9 m sin 23° = 0.74 m = h for the height of the incline. The work-kinetic energy theorem follows,
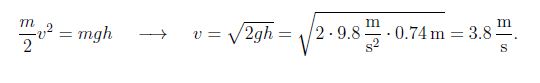
This result is remarkable in two ways:
(1) The speed is independent of the mass, so that all objects will reach the bottom at the end of the ramp.
(2) The final speed is independent of the angle a it is the same for an object sliding along the incline or freely falling object with θ = 90°.
While the final speed is independent of the angle θ, the time to reach the bottom of the ramp depends on the incline θ. We find the time from the kinematics equation for motion with constant acceleration a = g sin θ.