We consider the uniform motion of a point along a circle of radius A. Light produces a shadow on a screen. The motion of the shadow mimics harmonic motion, and angular velocity is related to the period, ω = 2π/T. The coordinate of the shadow is x = A cos(ωt). The magnitude of the object’s velocity on the reference circle is constant v = Aω . The component ofthe velocity vector along the screen is -Aω sin(ωt).
The magnitude of the (centriptal) acceleration of the object is ac = (Aω)2/A = Aω2 so that the acceleration of the shadow is a = – Aω2 A cos(ωt). Since a = -ω2 • A cos(ωt), we find, a = – ω2x.
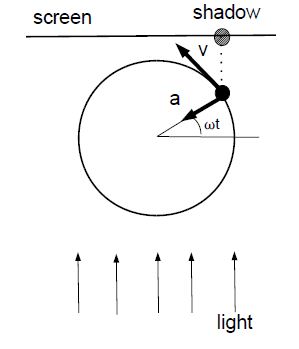
Since F = ma , the force follows, F = – mω2 x.
That is, the force is linear in the coordinate x. The force is negative, F < 0 [F < 0] when x > 0 [x < 0]; that is, the force drives the shadow back to the origin x = 0. We say that F is a linear restoring force. The period of oscillatory motion is independent of the amplitude of the motion.
Example: A pearl is moving in a bowl. a) Show that the force on the pearl is a linear for small angular displacements. b) Determine the period of harmonic motion of the pearl.
Solution: The weight of the pearl in tangential direction is given by Ftangentim = -mg sin ø. For small angles [in radians], sin ø ≠ sin ø, so that the force is given by
Ftangentim = – mg ø
That is, the force is proportional to the angular displacement. We write the tangential acceleration in terms of angular acceleration, a = Rα, where R is the radius of the bowl. Newton’s second law yields mRα = -mgϕ, or
α = -(g/R) ϕ
Comparison with F = – mω2 x, then yields ω = √(g/R), or for the period
T = 2π √(R/g).
Discussion: The condition of small angular displacement is not as limited as it may appear. For ϕ = π/6 [or ϕ = 30°], we have sin ϕ = 0.5 or sin ϕ ≈ ϕ within 5%. Fora bowl of radius R= 20 cm, the period follows T = 2π √(0.2 m)/(9.8 m/s2) = 0.9 s, which is easily verified at home.
We assume above that x = A at time t = 0. This is not the case in general, and instead we have for the ‘phase angle’ ϕ = ωt → ϕ0 + ωt. We then have for the coordinate, velocity; and acceleration:
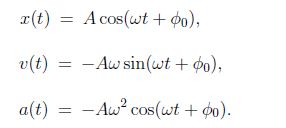
These equations can also be derived with methods from calculus [i.e., taking the derivates with respect to time t Vibe oscillatory motion is specified by the amplitude A and the initial phase ϕ0.