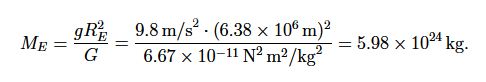The weight W = mg is the gravitational force that the Earth exerts on an object with mass (m). In general, there is an attractive force between two masses m1 and m2 separated by the distance r.
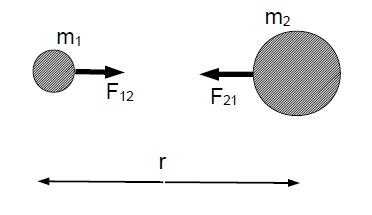
We have two masses m1 and m2. The forces F12 = – F21 are action-reaction pairs. The magnitude of the force is proportional to both masses and inversely proportional to the square of the radius r,
F12 = F21 = G (m1 m2 /r2)
Where, G = 6.67 x 10-11 N • m2/kg2 is the universal gravitational constant.
We consider the case of mass m and the Earth ME , so that m1 = m and m2 = ME . Since r = RE = 6.38 x 106 m is the radius of the Earth, we get for the mass of the Earth: mg = GME /RE2: