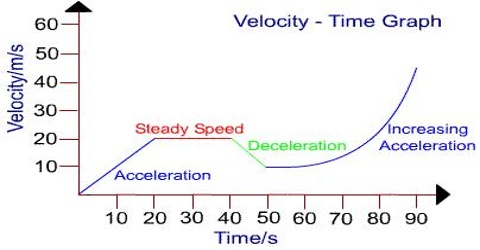
Velocity–Time graphs present the motion of an element by presentation the changes of velocity with reference to time. The law is that the slope of the line on a velocity-time graph reveals practical information about the acceleration of the object. If the acceleration is zero, then the slope is zero (i.e., a horizontal line). If the acceleration is positive, then the slope is positive (i.e., an upward sloping line).
Velocity-time graphs are used to explain the motion of objects which are moving in a straight line. They can be used to demonstrate acceleration and to work out displacement.
Velocity-time graph In case of uniform retardation and non-uniform acceleration
Velocity-time graph (In case of uniform retardation): There will always be initial velocity for uniform retardation. In this case, also the graph will be a straight line. But its slope will be negative [Figure]. A negative slope means retardation. The slope of the straight line becomes equal to the uniform retardation. Finally, the body comes to rest i.e., its velocity becomes zero.
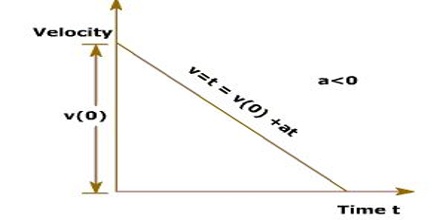
An object is said to be moving with uniform deceleration or retardation if it reduces its velocity by an equivalent amount in equivalent intervals of time. It is also known as uniform retardation. It is the acceleration in which the object changes its velocity with equivalent intervals of time. The angle of the velocity-time graph of an object moving with the uniform diminishing velocity with uniform acceleration is a downwards instantly line. The straight downward angle shows the decreasing velocity with uniform acceleration, i.e. retardation.
Velocity-time graph (In the case of non-uniform acceleration): In case of a body moving with non-uniform acceleration the velocity-time graph becomes a curve [Fig (a) and (b)]. Where velocity increases with time acceleration also increase as shown in Fig. (a) and Fig. (b)].
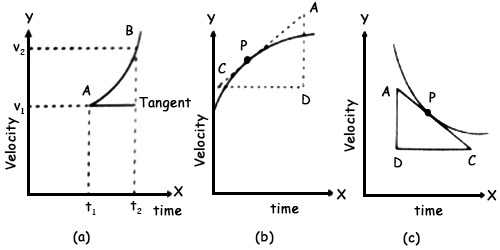
As before, it can be proved that during a time interval (t2 — t1) the average value of acceleration is equal to the slope of the area AB. Instantaneous acceleration at any point in the graph is equal to the slope of the tangent at that point. With the passage of time slope continues to increase. It is clear from it that acceleration is not constant [Fig. (c)], rather it increases with time. If the velocity of the body decreases with time or if there is retardation. Acceleration of point P is obtained from the slope of ∆ADC.
Acceleration = slope = AD/DC.
One excellent example of nonuniform accelerated motion is that of a mass bouncing at the end of a spring. This Simple Harmonic Motion has a velocity-time graph that is sinusoidal. It is the acceleration in which the object changes its velocity with uneven intervals of time.
Practical Example: A stone of mass ‘m’ is thrown straight upward from the top of a multi-story building with an initial velocity of +15 m/s. Find out the acceleration of stone just after it is thrown?
Answer: 10m/s² downward; A body in the air forever experiences a gravitational force in a downward direction. Thus the body is in the downward direction with a stable scale.