Vectors addition and subtraction in terms of components
A vector quantity can be resolved by parallelogram law into two or more vectors in different directions. The process of resolving a vector into two or more vectors is called resolution of a vector or vector resolution. Each resolving vector is called component of the original vector.
Resolution into perpendicular components:
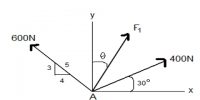
Let R be the vector along OB, so that OB = R. Now taking OB as diagonal let us draw the rectangle OABC [Fig. 1]. Here the components P and Q are perpendicular to one another, i.e.,
α + β = 900
then, Sin (α + β) = Sin 900 = 1 and;
Sin β = Sin (900 – α) = Cos α
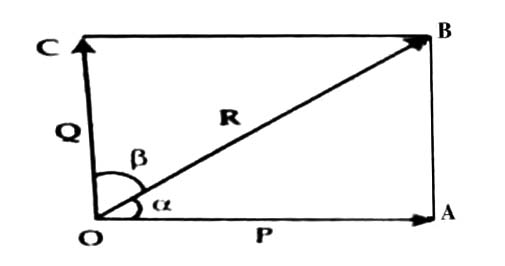
According to law at trainee at trigonometry we get from the triangle OAB.
P/Cos θ = Q/Sin θ = R/Sin 900
so, P = R Cos θ and Q = R sin α … …. ….. (1)
The two components P and Q are called the perpendicular components of the resultant R. P is called the horizontal component and Q is called tangential component.
Vector forms of the two components are –
P = R Cos α î + R Sin α î
So, their vector addition:
R = P + Q = R Cos α î + R Sin α î … …. ….. (ii)
and vector subtraction will be the vector subtraction of P and Q.

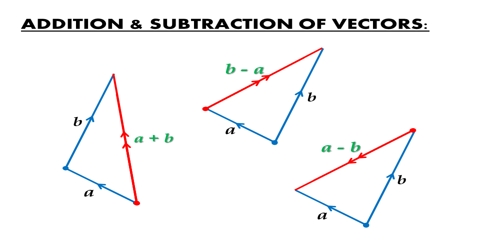
Example: Suppose P is acting along the arm AB and is acting along the arm BC of the triangle [Fig. b). Then their vector addition R = P + Q, may be represented by the third arm AC of the triangle. Again, if P and Q are acting along AB and BC then vector subtraction R = P – Q, can be represented by the third arm CA of the triangle.