Unit Vector: A vector whose magnitude is unity is called a unit vector.
When a vector of non-zero magnitude is divided by its magnitude it gives a unit vector along the direction or parallel to the direction of that vector.
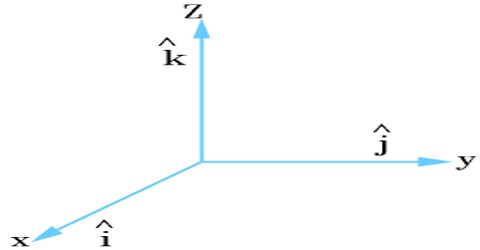
In order to describe a unit vector normally a hat sign (^) is put on the small letter. For example, ȋ, ĵ, ƙ etc are used for denoting unit vector.
Let Ā be a vector whose magnitude. A ≠ 0
So, Ā/A = unit vector along the direction of Ā = â (suppose).
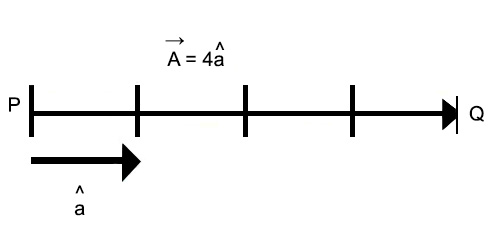
So, if the magnitude of a vector Ā is A = 4 unit, and if â is the unit vector along the direction of A. then Ā = 4 â (figure)
That means if the magnitude of a vector is multiplied by its unit vector, then we get the vector.