Triangular law of forces states that if there are two forces which are congregation or transient through a point then the third or enclosing side of a triangle is such that. So, this law explains, if two forces stand-in at a point is represented in scale and direction by the two adjacent sides of a triangle taken in order, then the closing side of the triangle taken in the reversed order represents the consequential of the forces in magnitude and direction.
The resultant of two forces acting at a point can also be found by using the Triangle Law of Forces.
If two forces acting at a point are represented in magnitude and direction by the two adjacent sides of a triangle taken in order, then the closing side of the triangle taken in the reversed order represents the resultant of the forces in magnitude and direction.
The triangle law of forces can also be stated as. if a body is in equilibrium under the action of three forces acting at a point, then the three forces can be completely represented by the three sides of a triangle taken in order.
Explanation
A body might be subjected to further than one force at a similar time. Suppose two equal forces are acting on the body at the same time, in the same way, the consequence is the sum of the two forces. But if the similar forces are accurately in reverse directions, they rescind with each other and therefore almost there is no effect on the body.
So, we learn that, if three forces, stand-in at a point, are represented in magnitude and way by the sides of a triangle, taken in order, they will be in equilibrium.
Forces P and Q act at an angle 0. In order to find the resultant of P and Q. one can apply the head to tail method, to construct the triangle.
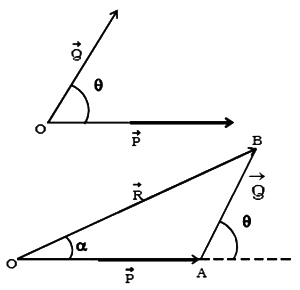
In Figure, OA and AB represent P and Q in magnitude and direction. The closing side OB of the triangle taken in the reversed order represents the resultant R of the forces P and Q. The magnitude and the direction of R can be found by using sine and cosine laws of triangles.
If P, Q, and R are the three forces acting at a point and they are represented by the three sides of a triangle then, P/OA = Q/AB = R/OB.
Mathematical Explanation –
Forces stand-in at a position can be determined into a series of three forces that might be represented by a triangle. Take any two (adjacent) forces and parallel the third force from one of the ends of the vectors forming those two forces. If that third parallel force vector matches the course and size of the third side of the triangle formed, the forces are in equilibrium.
Formula:
a/sin A = b/sin B = c/sin C
Where,
- a, b, c = sides of a triangle
- A, B, C = angles between the sides of a triangle.
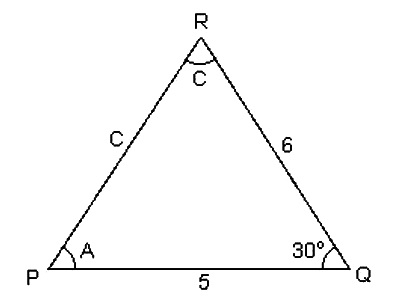
Find angle A, C and side c from side a = 5, side b = 6, angle B = 30 using triangle law of forces.
Solution:
Let us estimate the value of angle A from angle B.
Step 1:
In the given formula, take sin A on left hand side and multiply a with sin B divided by b which gives,
sin A = (a x sin B) / b = (5 x sin 30) / 6
A = sin-1(0.4167) = 24.6240
Step 2:
Angle, A + B + C = π
Therefore, C = π – A – B
C = 180 – 24.624 – 30 = 125.3760
Step 3:
To calculate the value of c:
In the given formula, take c on left hand side and multiply a with sin C divided by sin A which gives,
c = (a x sin C) / sin A
c = (5 x sin 30) / sin 24.624 = 9.784.