Trajectory of Projectile Motion is a Parabola
If you go to a stadium to enjoy cricket game then you will see that the cricket ball thrown from the boundary is seen to be ascending first and then comes back to the ground in a curved path. Similar phenomena are observed in case of motion of bullet fired upward from a gun, motion of arrows, bomb thrown from plane— in all cases same type of trajectories are observed.
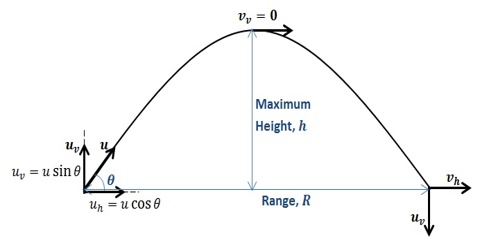
This type of curved motion is called motion of projectile and the path is called trajectory. It is a parabola. This type of motion is two dimensional motion. If we ignore air-resistance motion of a projectile in due gravity only path of projectile is always parabolic. When the projectile reaches the maximum height, its velocity becomes minimum. Again, the motion of the projectile at maximum height is one dimensional. Maximum distance that a projectile travels horizontally is called the range of the projectile. Acceleration along horizontal, ax = 0, and Vertical acceleration ay = – g. At the point of ejection the coordinate of the origin is x = 0, y = 0. Suppose a projectile is thrown from point O vertically at an angle of θ with initial velocity v0 (Figure). Initial velocity of the projectile v0 can be resolved into two components. One component along OX and the other one along OY.
 The two components are;
The two components are;
vx0 = v0 cos and vy0 = sin θ
We can count time from the instant of ejection i.e., if distance travelled in time t = 0 is x, then according to the equation of motion, x = vx0 t + ½ ax t2
x = v0 cos θt + 0 [Horizontal motion vx0 = v0 cos θ]
so, t = x / [v0 cos θ] … … … (1)
Again, as ax = – g, so after time t this velocity of the projectile in the vertical direction,
vy = vy0 – gt = v0 sin θ – gt … … … (2)
If after time t, the projectile reaches to a height y then,
y = vyot – ½ gt2 = v0 sin θ t – ½ gt2 … … … (3)
Resultant velocity at time t, v = √(vx2 + vy2)
If the resultant velocity makes an angle α with the horizontal, tan α = vy/vx
Putting the value of t in equation (3) we get,
y = (v0 sin θ) [x/(v0 cos θ)] – ½ g [(x2 / v02cos2θ)]
so, y = (tan θ)x – [(g /2 v02cos2θ) x2
y = ax — bx2
This is the equation of a parabola.
Here a = tan θ, b = g /2 v02cos2θ
These two quantities are constant in the path of ejection. So trajectory of a projectile is a parabola.