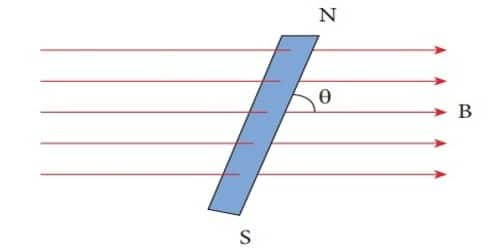
Consider a bar magnet NS of length 2l and pole strength m placed in a uniform magnetic field of induction B at an angle θ with the direction of the field (Figure). A uniform magnetic field can be prepared by making a comparatively long cylindrical coil.
Due to the magnetic field B, a force mB acts on the North Pole along the direction of the field and a force mB acts on the South Pole along the direction opposite to the magnetic field. The space or region around a magnet or a wire carrying current whereby the magnetic needle shows deflection, that space or region is called the magnetic field of that magnet or wire carrying current.
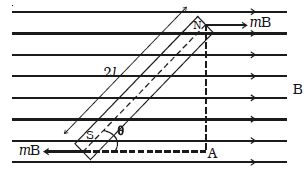
These two forces are equal and opposite, hence constitute a couple.
The torque τ due to the couple is
τ = one of the forces x perpendicular distance between them
τ = F x NA
= mB x NA … …. (1)
= mB × 2l sin θ
so, τ = MB sin θ
Vectorially, τ = M x B
The direction of τ is perpendicular to the plane containing M and B.
If, B = 1 and θ = 90 θ
Then from equation (2), τ = M
Hence, the moment of the magnet M is equal to the torque necessary to keep the magnet at right angles to a magnetic field of unit magnetic induction.