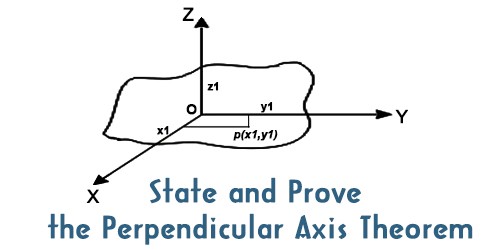
The theorem states that “the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in its plane and intersecting each other at the point where the perpendicular axis passes through it.”
This theorem states that the moment of inertia of a planar body about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body. Perpendicular axis is used to find the moment of inertia for a solid object that lies about an axis perpendicular to the plane is equal to the sum of the moment of inertia of two perpendicular axes lying in the same point within the plane.
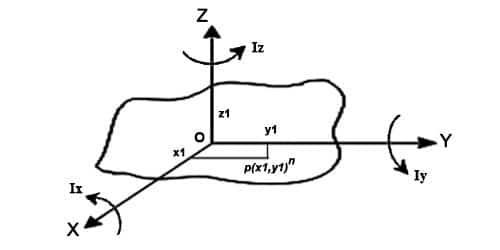
Fig: Prove of the perpendicular axis theorem
Explanation: Let OZ be the axis perpendicular to the plane lamina and passing through point O. Let OX and OY be two mutually perpendicular axes in the plane of the lamina and intersecting at point O. If Ix, ly and lz are the moments of inertia of the plane lamina about the axes OX, OY and OZ respectively, then according to the theorem of perpendicular axes, Iz = Ix + ly.
This theorem is appropriate only to the planar bodies. Bodies which are flat with very less or insignificant thickness. Using the perpendicular axis theorem, you can analyze the area moment of inertia about an axis when the area moment of inertia about two other mutually perpendicular axis to that point is known.
Proof: Let, the lamina consists of n number of particles of masses m1, m2, m3, … mn.
and their positions are at the distances r1, r2, ……rn respectively from the origin O.
For simplicity, let a particle of mass m1, is at point P (x1, y1) and its position is denoted by r1.
So, r12 = x12 +y12
The moment of inertia of the particle of mass m, about OZ axis is,
I1 = m1r12 = m1 (x12 + y12)
Similarly, the of inertia of the particle of mass m2 about OZ axes is, I2 = m2 (x22 + y22) Therefore, the moment of inertia of the whole lamina about OZ axis is,
Iz = I1 + I2 + …….. + In
= m1 (x12 + y12) + m2 (x22 + y22) + …….. + mn (xn2 + yn2)
= (m1x12 +m2x22 +…..+ mnxn2) + (m1y12 +m2y22 +…..+ mnyn2)
So, Iz = Ix + ly [Proved]
Conclusion
This theorem is most useful when considering a body which is of a regular form (symmetrical) about two out of the three axes. If the moment of inertia about these axes is known then what about the third axis may be calculated. The utility of this theorem goes beyond that of calculating moments of strictly planar objects. It is a valuable tool in the building up of the moments of inertia of three-dimensional objects such as cylinders by breaking them up into planar disks and summing the moments of inertia of the composite disks.
The theorems not only help us in finding the mass moment of inertia but also in finding the area moment of inertia (with a few changes). Thus, this theorem has broad applications in planar dynamics and helps to solve problems in a faster and easier way.