Scalar or Dot Product
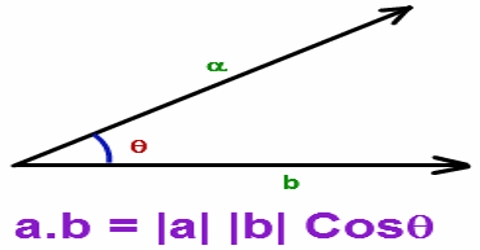
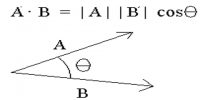
The scalar or dot product of two vectors is a scalar quantity equal to the product of the magnitudes of the two vectors and the cosine of the angle between them. It is expressed by inserting a dot (•) sign between the two vector quantities and read as “first quantity dot second quantity”.
The scalar quantity that is obtained due to the product of the two vector quantities is called the scalar product of the two vectors. Or, the product of the magnitudes of the two vectors when multiplied by their cosine of the angle between them, then that product is called the dot product or scalar product.
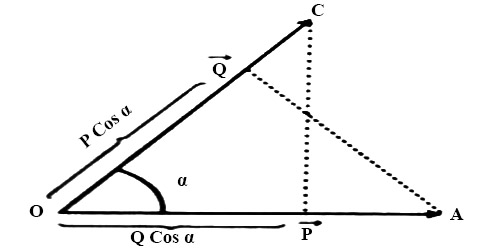
Explanation: Let P and Q represent two Vectors. Arrow marked straight lines OA and OC indicate magnitude and direction of the two quantities (Figure). These are inclined to each other at an angle α. P→.Q→ indicates their scalar or dot product and read as P dot Q. According to the definition dot product of the two vectors is,
P→.Q→ = |P→|.|Q→| Cos α
or, P→.Q→ = PQ Cos α = QP Cos α … … … (i)
Here, 0 ≤ α ≤ π
But, Q Cos α is the component of Q in the direction of P or projection of Q on P and P Cos α is the component of P→ in the direction of Q→. (in figure)
Again, P.Q = PQ Cos α = Q (P Cos α)
But P Cos α, is the component of P→ in the direction of Q→ or projection of P→ on Q→.
So, scalar product of two vectors means the product of the modulus or magnitude of a vector and component of the other vector in the direction of the first one or projection of the other vector on the first vector.
It is seen from equation (i) that the product is a scalar quantity.