Relation between Surface Tension and Surface Energy
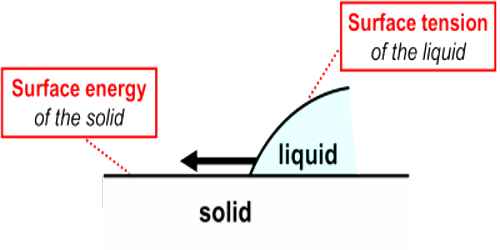
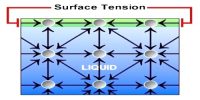
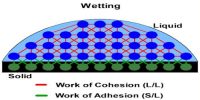
Surface energy is the work per unit area done by the force that creates the new surface. The cohesive forces between liquid molecules are responsible for the phenomenon known as surface tension. In order to find the relation between surface tension and surface energy, consider a film of liquid produced in a rectangular frame ABCD of which the cross piece BC of length L can slide freely along the length AB and DC.
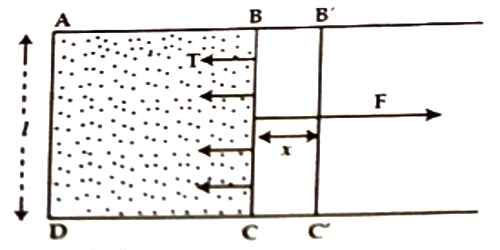
Since a liquid surface behaves like a stretched membrane and tends to contract, surface tension will act at every point of BC at right angle to it and tangential to the surface of the film (Figure). Due to the action of this force the arm BC will slide towards AD of the frame. To keep the wire fixed to its position an equal force is to be applied in the opposite direction. If surface tension = T and length of BC = l, so, inward force on BC due to surface tension is,
F = 2l x T
Since the film has two surfaces, one toward top and the other one at the bottom, hence length or BC = 2l. In order to keep BC steady an equal force opposite to surface tension is to be applied.
The force required to keep the wire fixed to its position, F = 2lT
Now, the arm BC is moved, very slowly, at a distance x perpendicular to its length to position B՛C՛, the work done against the surface tension is,
W = Force x Displacement = F x X = 2lTx (we know, F = 2/T)
So, the work done to increase the surface area of the film by unity = Work/Increase of area
= W / (2/x) = (2lTx) / (2lx) = T
where 2lx is the total increase of area (2 is taken for upper and lower surfaces of the film)
But work done to increase the surface area by unity = potential energy stored by per unit area = surface energy.
So, we can conclude that the surface tension is numerically equal to the surface energy.
Now, if surface tension = T and surface energy = E
Then, E = T
Example Work: What will you see if a ring of wire is dipped inside soap-solution and then brought it out? You will see a thin film of soap inside the ring. Keep a loop made of thread on that film. What will you see? How will the loop stay on the film?
When the loop is placed on the film, equal and opposite internal and external tangential force will act on each point of the loop. These two forces balance each other, so the loop will stay on the film in circular shape.