Relation between electric intensity and electric potential
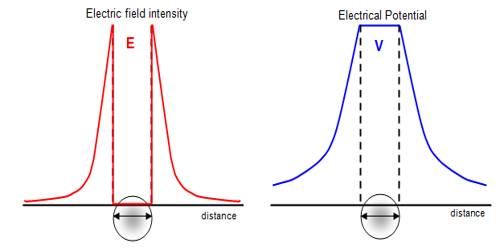
The electric force acting on a unit charge at a point in the electric field is called electric field intensity. It is also called field intensity. And the electrical state for which flow of charge between two charged bodies takes place is called electric potential.
Let A and B be two close points in an electric field [Figure] and let the electric potentials be respectively VA and VB. If VA > VB, then the potential difference = VA – VB.
Since the points are very close to each other, the electric field there may be taken to be the same and let it be E.
Work done in bringing, a unit positive charge from B to A
= Electric field intensity, E x distance AB
But, we know the Work done in bringing a unit positive charge from B to A is equal to the potential difference between the two points.
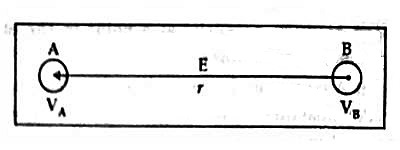
We get, E x AB = VA – VB
or, E = (VA – VB) /AB = (VA – VB) /r
where r is the distance between the points A and B.
or, E = V/r, where, VA – VB = ΔV = V … … … (1)
By calculus wean write,
E = – dV/dr
Here negative sign indicates that for the increase of potential difference displacement of the charge is to be in the opposite direction of the electric field.
From the above equation, it is inferred that the electric field intensity at any point in the electric field is equal to the rate of change of potential difference with respect to distance.
dV/dr is called potential gradient.
Unit: According to equation (1), S. I. unit of E is volt/meter (V/m or Vm-11).
So, we get two units of E, viz- (i) Newton/Coulomb (NC-1) and (ii) volt/meter (Vm-1).