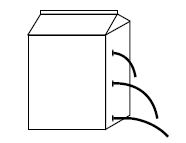
Pressure at a point in a liquid means a force exerted perpendicularly by the liquid on unit area around that point in the liquid. In figure (1) some liquid is kept in a vessel.
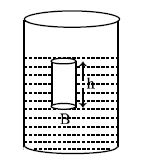
Figure (1)
Let the area of the base of the vessel =A
density of the liquid = p
depth of the liquid = h
acceleration due to gravity = g
We know, pressure = force / area
Now, the force acting on area A = weight of the liquid
= mass of the liquid x g
= volume of the liquid x density x g
= area of the base x depth x density x g = Ah pg
Pressure, P = Ahpg/A
or, Pressure, P= hpg
Again as `g,’ is a constant, so P ∞ hp
i.e. the pressure at a point in a liquid at equilibrium is directly proportional to the depth of that point from the free surface of the liquid and its density. Therefore pressure rises with the increase of depth of the liquid and also increase in density causes the rise of pressure. As pressure rises with the increase of depth, the liquid comes out with more speed from a hole at greater depth (shown in the figure).