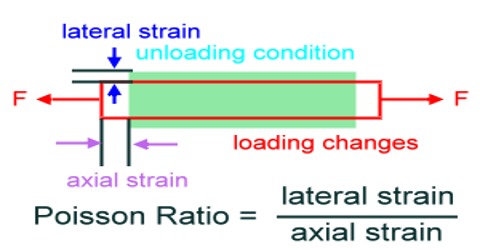
Poisson’s Ratio is the ratio of the proportional decrease in a lateral measurement to the proportional increase in length in a sample of material that is elastically stretched. This was discovered by scientist Poisson. According to his name this constant is called Poisson’s ratio.
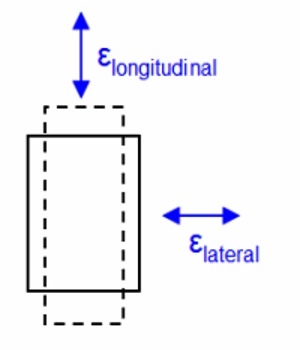
Whenever a body is subjected to a force in a particular direction, there is change in dimensions of the body in the other two perpendicular directions. This is called lateral strain.
If a wire is fixed at one end and a force is applied at the other end, it is observed that lateral strain occurs along with longitudinal strain, that is, the length increases and radius of the wire decreases. According to Poisson’s experimental results, within elastic limit, the ratio of lateral strain to longitudinal strain is called Poisson’s ratio.
[Lateral strain / Longitudinal strain] = Constant
It is denoted by σ. It is called Poisson’s ratio.
so, [Lateral strain / Longitudinal strain]
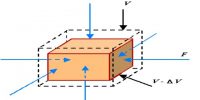
Explanation: Consider a wire of initial length L and radius r (figure). The wire is fixed at one end and a force ‘F’ is applied at the other end. Consequently, the length of the wire will increase and radius will decrease. Let the final length of the wire be L′ and final radius, f′.
So, increase in length, ∆L = L′ – L and,
Decrease in radius, ∆r = r – r′
Hence, lateral strain = ∆r/r
Poisson’s ratio, σ = [Lateral strain / Longitudinal strain]
(∆r/r) / (∆L/L) = (L/r) x (∆r/∆L)
If ∆L is positive, ∆r becomes negative and vice versa.
So, σ = – (L/r) x (∆r/∆L)
Poisson’s ratio is the characteristic of solids only.
Value of σ: The value of σ of material lies between -1to ½, i.e., – 1 < σ < ½.
Unit and Dimension of σ: As σ is a ratio of two strains, so it has no unit or dimension.
Significance: Poisson’s ratio describes the relationship between strains in different directions of an object. It is a useful constant that tells us what will happen when we compress or expand materials.
“The Poisson’s ratio of copper is 0.33”. This statement means that within elastic limit the ratio of lateral strain to longitudinal strain of copper is 0.33.
The value of σ can be less than – 1 and cannot be more than ½. That means the value of σ is in between – 1 ½. Actually, it is seen that the value of σ is within 0.2 to 0.4.