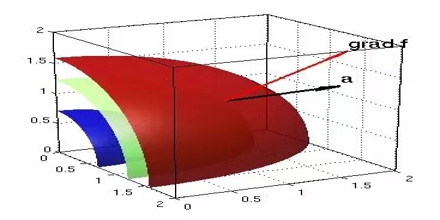
Gradient tells you how much something changes as you move from one point to another (such as the pressure in a stream). The gradient is the multidimensional rate of change of a particular function. The gradient vector is a representative of such vectors which present the value of differentiation in all the 360° direction for the given point on the curve”
The gradient is a vector function which operates on a scalar function to produce a vector whose scale is the maximum rate of change of the function at the point of the gradient and which is pointed in the direction of that utmost rate of change. The symbol for the gradient is ∇.
(i) A gradient of a scalar quantity is a Vector quantity.
(ii) The magnitude of that vector quantity is equal to the Maximum rate of change of that scalar quantity.
(iii) Change of scalar quantity does not depend only on the coordinate of the point, but also on the direction along which the change is shown.
For the gradient of a vector field, you can think of it as the gradient of each component of that vector field individually, each of which is a scalar. The gradient always points in the direction of the maximum rate of change in a field.
Physical Significance of Gradient
A scalar field may be represented by a series of level surfaces each having a stable value of scalar point function θ. The θ changes by a stable value as we move from one surface to another. These surfaces are known as Gaussian surfaces. Now let the two such surfaces are very close together, be represented by two scalar point functions and (θ + d θ). Let ‘r’ and (r + d θ) be the position vectors of points A and B, on the surfaces θ and (θ + d θ) correspondingly with respect to an origin 0 as shown in Figure. Clearly, the vector AB will be dr. Let the least detachment between the two surfaces ‘dn’ be in the direction of unit usual vector n at A.
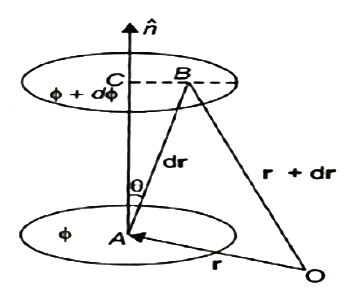
dn = dr cos θ
= | n | dr | cos θ =n .dr
Dϕ = ∂ϕ/ dn =∂ϕ/dn n .dr…… (1)
Since the continuous scalar function defining the level surfaces (Gaussian surfaces) has a value θ at point A (x, y, z) and (θ + dθ) at point (x + dx, y + dy, z + dz), we have
dϕ = ∂ ϕ/dx dx +dϕ/∂y + ∂ϕ/∂x dz
= (I ∂ϕ/∂x +j ∂ϕ/vy +k ∂ϕ/∂z) .(idx +jdy +kdz)
= ∆ ϕ. dr … … (2)
From equations (1) and (2), equating the values of d θ,
We obtain ∆θ .dr =∆ ϕ= ∂ϕ/ ∂n n .dr
As dr is an arbitrary vector, we have
∆ϕ =∂ϕ/∂ n
Grad ϕ = ∂ ϕ/∂n n
Therefore, the gradient an of a scalar field at any point is a vector field, the scale of which is equal to the highest rate of increase of θ at that point and the direction of it is similar as that of usual to the level surface at that point.