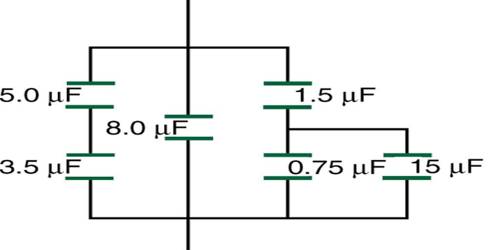
Parallel Combination of Equivalent capacitance
Parallel combination: When some capacitors are connected in such a way that the first plate of each capacitor is connected to one point and the second plate of each capacitor is connected to another point then the combination or grouping is called parallel combination.
In the figure, three capacitors of capacitances C1, C2 and C3 are connected in parallel combination. The first plate of each capacitor is connected to a point M and the second plate of each capacitor is connected to the earthed point N. In this condition, if Q amount of positive charge is given to point M, the potential difference between the plates of each capacitor will be same and U charge will be distributed to different capacitors according to their capacitances.
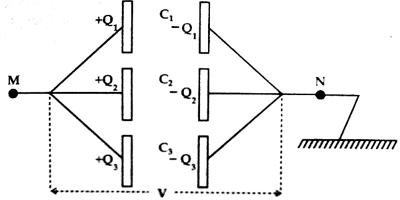
Let charges in C1, C2 and C3 be respectively Q1, Q2 and Q3 and potential difference between M and N be V. Then,
Q1 = C1V, Q2 = C2V and Q3 = C3V
and Q = Q1 + Q2 + Q3
so, Q = C1V + C2V + C3V
= (C1 + C2 + C3)V
If, instead of total parallel combination, a capacitor of capacitance CP is connected between the points M and N and Q amount of positive charge is given to M and the potential difference between M and N is V, then,
QP = CPV = (C1 + C2 + C3)V
So, CP = C1 + C2 + C3
CP is the equivalent capacitance.
Similarly, we can show that for the parallel combination of n number of capacitors of capacitances C1, C2, C3, … … , Cn, the equivalent capacitance CP is given by,
CP = C1 + C2 + C3 + … … … + Cn
So, the equivalent capacitance of parallel combination of capacitors is equal to the algebraic sum of individual capacitances.sub