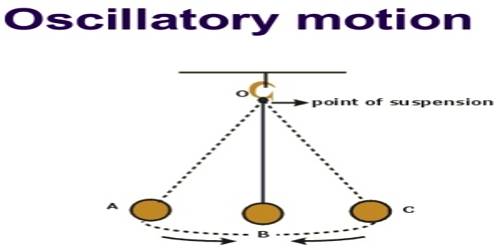
Oscillatory Motion
A particle having periodic motion remains half of its time period in one direction and the rest of time period remains in other direction along the same line, then its motion is called oscillatory motion. It is the motion of the oscillating body around its rest point, where the motion is repeated through the equal intervals of the time.
Example: Motion of simple pendulum, the motion of strings of a guitar, oscillation of air-particles during the transmission of sound etc. The clock, tuning fork, spring, stretched string, the motion of the swing etc. are the example of Oscillatory Motion.
In the absence of friction, the oscillatory motion would continue forever; but in the real world, the system eventually settles into equilibrium. Oscillation of a particle having the periodic motion is a sine wave which contains terms like amplitude, angular frequency and time. The equation of a particle at periodic motion towards X-axis is,
x = a sin ωt
here, α amplitude, ω m angular frequency, t = time.
In the following [figure (c)] the equation has been shown by a graph.
Fig: A2