For an object in the gravitational field of the Earth, the mechanical system is the object and the Earth. The force [interaction] is described by a potential energy energy: we say that the system is closed. Not all interactions can be described in this manner. Since the (kinetic) friction force is always opposing the displacement, the work done kinetic friction force is negative. In particular, the work is non-zero when the object returns to its starting position, and we conclude that (kinetic) friction is a non-conservative force. Systems for which interactions are described by non-conservative forces are called open systems.
Example: An object with mass m = 3.2 kg sits on an incline plane at an angle θ = 23°. The object slides down the incline with s = 1.9 m, starting from the rest and travelling at the speed v = 2.1 m/s at the end of the ramp. Find the coefficient of kinetic frcition between the object and the ramp.
Solution: We find the mechanical energy when the object is on the top of the ramp and at the bottom,
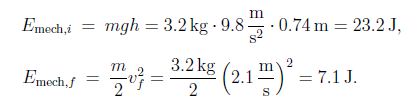
We thus find the work done by the friction force,
Wnc = 7.1 J – 23.2 J = -16.1 J,
so that for the friction force
fk = – (Wnc/s) = – (- 16.1 J / 1.9 m) = 8.5 N
The normal force is given by FN = mg cos θ = 3.2 kg 9.8 m/s2 cos 23° = 28.9 N. Since fk = μk*FN, we find the coefficient of kinetic friction,
μk = fk / FN = (8.5 N / 28.9 N) = 0.29
This is a reasonable value for the coefficient of kinetic friction.