Motion of a Simple Pendulum is Simple Harmonic Motion (SLIM)
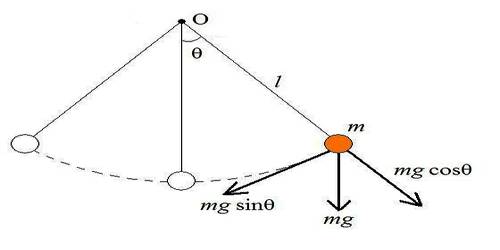
Almost a valueless body suspended by a weightless, soft and non-compressible thread from a rigid support is allowed to oscillate in simple harmonic motion from a simple pendulum. If this pendulum is allowed to oscillate within 4°, then its motion will be simple harmonic motion. In figure this type of simple pendulum has been shown.
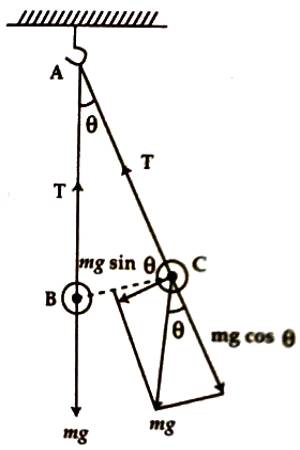
Suppose AB is a simple pendulum and its centre of mass is B and ‘m’ is its mass. When the pendulum is allowed to oscillate, then at some moment it comes to position AC making an angle θ with the equilibrium position. Now, weight mg of the point C acts vertically downward. This weight can be resolved into two components. One component along the length of the thread CD is mg cos θ and the other component is opposite to the displacement along CE is CE mg sin θ. Here component mg sin θ is balanced by the tension T of the thread. Only effective force F is mg sin θ whose direction is along the equilibrium position.
F = – mg Sin θ …. …. (1)
Here g = acceleration due to gravity. Since force is opposite to displacement, so negative sign has been used.
Now, if a is the acceleration of the effective force, then F = ma •••
so, ma = – mg sin θ
or, a = – g sin θ …. …. (2)
If the value of θ is small (less than 40), then it is assumed that sin θ = θ radian.
In that case, locus of the simple pendulum becomes linear.
From equation (2) we get a = – g x BC/AC = – g x (x/L)
Here if g/L = constant = ω2 then a = ω2x or, a ∞ – x
That means, acceleration is proportional to displacement and is oppositely directed, which expresses the characteristics of simple harmonic motion. Time period of an oscillating simple pendulum can be found by using, the above equation.
We get, ω2 = g/L
or, ω = √(g/L)
We know, ω = 2πn and T = 1/n
or, 2πn = √(g/L)
or, 2π (1/T) = √(g/L)
so, T = 2π √(g/L) … … (3)
It is the equation of time period of simple harmonic motion. It the time period of simple pendulum, T = 2 sec. then we Call that pendulum as second pendulum. From equation (3) we get,
g = 4π2 (L/T2)
That means, motion of a simple pendulum with small amplitude (less than 4°) is the motion of a simple harmonic motion.