Lens Maker’s Formula or Equation of Lens Formation
The lens maker’s equation is a formula used for lenses gives us a relationship between the focal length, refractive index, and radii of curvature of the two spheres used in the lens.
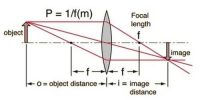
Let AB be a principal section of a thin lens [Figure). P is a point object on its principal axis OP and O is its optical center. Suppose an incoming ray of light PM through the air is incident at point M, a small distance from the optical center of the lens and is refracted along MN in the first surface and is incident at point N in the second surface and is refracted along NR.
Again, the ray PO from the point passing through the principal axis is refracted along the same line in an air medium. So, the intersecting point p of the above two rays is the virtual image of the object P. This is because that if these rays are looked at from the other side of the lens, they will appear to have come from that point.
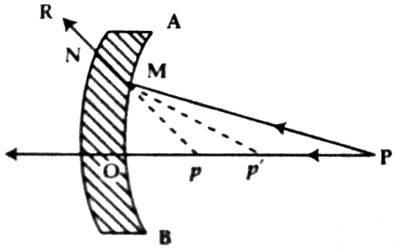
Suppose due to an extension of NM backward, it intersects PQ at point pʹ. Then pʹ will be the virtual image of point P due to refraction in the first spherical surface and will act as the virtual object with respect to the second surface. So, p will be the image of pʹ due to refraction in the second surface.
Let the distance of the object OP = u, the distance of the image = v and OPʹ = vʹ, and the radii of curvature of the first and second spherical surfaces be r1 and r2, respectively. Let refractive index of the material of the lens with respect to air = μ.
Now, according to the real positive convention of the sign, the image pʹ produced for P in the first spherical surface may be written as-
μ/vʹ + 1/μ = (μ – 1)/r1 … … … (1)
and the image p produced for pʹ in the second surface may be written as,
(1/μ) / v + (1/-vʹ) = (1/μ – 1) / r2 [the object is virtual, here vʹ is negative]
By multiplying both sides by µ we get,
1/v – μ/vʹ = – (μ – 1) / r2 … … … (2)
By adding equation (1) and (2) we get,
1/v + 1/μ = (μ – 1) (1/r1 – 1/r2) … … … (3)
The equation (3) represents the relation between the distance of the object, distance of the image and the radius of curvature of the lens.
An equation for the toed length of the lens: If the object is at infinity, then its image will be formed at the second principal focus of the lens. In this case, μ = ∞, and v = ƒ. From equation (3) we get,
1/ƒ + 1/∞ = (μ – 1) (1/r1 – 1/r2)
or, 1/ƒ – 0 = (μ – 1) (1/r1 – 1/r2)
So, 1/ƒ = (μ – 1) (1/r1 – 1/r2) …. …. …. (4)
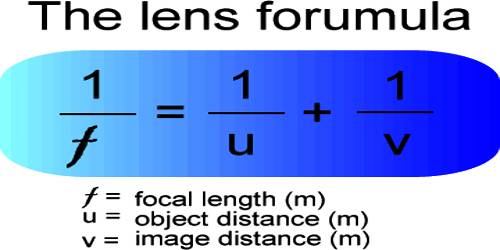
This is the general equation of the focal length of a lens.
If the refractive index of the surrounding medium is μ1 and the refractive index of the material of the lens is μ2 then inserting μ2/μ1 in place of μ in equation (4) we get,
1/ƒ = (μ2/μ1 – 1) (1/r1 – 1/r2)
This is called the lens maker’s formula. It is also called the formula for the focal length of the lens. It is determined by the medium of the lens, surrounding medium and the radii of curvature of the two surfaces of the lens.