Length Contraction according to the Theory of Relativity
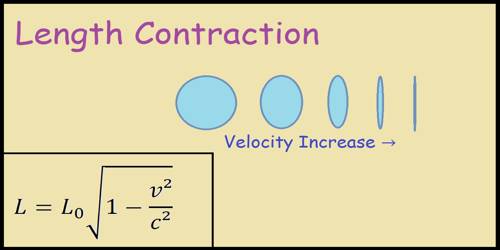
According to classical mechanics, whatever may be the velocity of the observer with respect to the object or whatever may be the velocity of the object with respect to the observer, length of a body will remain same to all observers. But according to the theory of relativity, if there is a relative velocity between the object and the observer length of an object will be short to an observer. This is called length contraction.
The length of a moving object becomes less than that of the stationary state. This phenomenon is called length contraction.
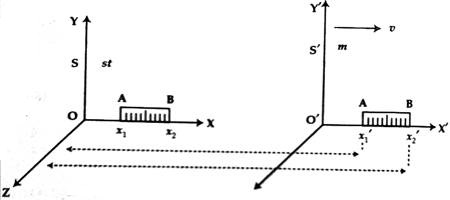
Determination of Length contraction: We know, the distance between the two ends of an object is its length. Let us consider two frames of reference. One is S and the other one is Sˊ [Fig]. Here the frame S is stationary. Let us represent it by ‘st’ and the frame Sˊ is moving which is represented by m. Let us consider the rod AB at rest.
Let us consider that the rod is lying along the X-axis in the ‘st’ frame. An observer in this frame determined the coordinates of the ends of the rod as x1 and x2. According to him, the length of the rod, LO = (x2 – x1). This length is the actual or intrinsic length i.e., the length obtained at rest with respect to the observer. The ‘m’ frame is in motion with a velocity of ‘v’ with respect to frame ‘st’. An observer in that frame determined the coordinates of the ends of the rod as x1ˊ and x2ˊ. So, according to the observer, the length of the rod, L = (x2ˊ — x1ˊ).
According to the Lorentz’s inverse transform,
x2 = (x2ˊ + vt) / √(1 – v2/c2) … … … (1)
x1 = (x1ˊ + vt) / √(1 – v2/c2) … … … (2)
Subtracting equation (2) from equation (1) we get,
(x2 – x1) = (x2ˊ — x1ˊ) /√(1 – v2/c2)
Again, L0 = L / √(1 – v2/c2)
or, L = L0 √(1 – v2/c2) … … … (3)
From equation (3) it is proved that. L0 > L. i. e., the length of a rod measured in moving condition will be less than the length measured at rest. This phenomenon is called the Lorentz Fitzerald contraction.
So, to the observer in ‘S’ it would appear that the length of the rod in Sˊ has contracted by the factor √(1 – v2/c2).