The vibrations created by a string are nothing but a wave. A string is a tight wire. When it is plucked or bowed, progressive transverse waves move along the wire and is reflected at the fixed ends. A progressive sound wave is formed in the adjacent air having a frequency equivalent to that of the stationary wave in the string. These waves superpose with the incident waves and produce a stationary wave in the wire. The sound produced by a string has almost the same frequency.
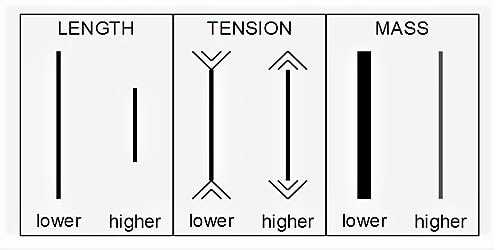
There are three laws in the case of the vibrating string. The laws of transverse vibrations of stretched strings are (i) the law of length (ii) law of tension and (iii) the law of mass.

- Law of length
First law tells that when the tension and the linear density are constant, the frequency of the vibration is inversely proportional to the length. For a given wire tension (T) and linear density (m) are constant, the fundamental frequency of vibration (n) is inversely proportional to the vibrating length (l),
i.e. n ∞ 1/l
or, nl = constant.
The fundamental frequency of vibration of a string (fixed at both ends) is inversely proportional to the length of the string provided its tension and its mass per unit length remain the same.
- Law of tension
The second law states that, if the length and linear density are constant, the frequency is directly proportional to the square root of the tension. For the length (l) and linear density (m) are constant, the fundamental frequency (n) is directly proportional to the square root of the tension (T),
i.e. n ∞ √T
or, n / √T = constant.
The fundamental frequency of a string is proportional to the square root of its tension provided its length and the mass per unit length remain the same.
(iii) Law of mass
The third law is that, when the length and tension are constant, the frequency is inversely proportional to the square root of linear density. The fundamental frequency of a string is inversely proportional to the square root of the linear mass density, i.e., mass per unit length provided the length and the tension remain the same.
(iii) For the length (l) and tension (T) are constant, the fundamental frequency (n) varies inversely as the square root of the linear density (m),
i.e. n ∞ 1/√m
or, n√m = constant.
The laws of transverse vibration of the stretched string are verified by using sonometer