Isothermal Expansion of Carnot Cycle:
Let consider one mole of an ideal gas enclosed in the cylinder. Let V1, P1 be the initial volume and pressure of the gas respectively. The initial state of the gas is represented by the point A on the P-V diagram. The cylinder is placed over the source which is at the temperature T1.
The piston is allowed to move slowly outwards, so that the gas expands. Heat is gained from the source and the process is isothermal at constant temperature T1. In this process the volume of the gas changes from V1 to ; and the pressure changes from P1 to P2. This process is represented by AB in the indicator diagram (Figure).
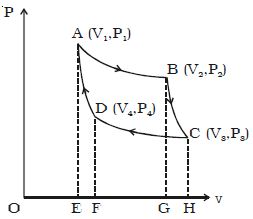
During this process, the quantity of heat absorbed from the source is Q1 and W1 is the corresponding amount of work done by the gas.
Q1 = W1 = v2∫v1 PdV =RT1 loge (V2/V1)
= Area ABGEA