Four Steps in Carnot’s Engine
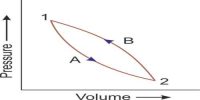
The Working of a Carnot’s cycle and work was done by it can be expressed in a curve. It is called index curve. In the following index curve explanation of different actions and the calculation of work done by a Carnot’s cycle have been given.
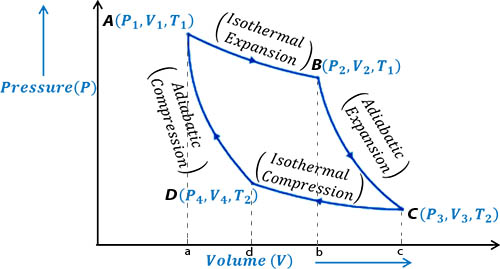
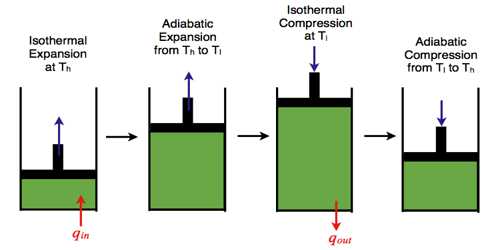
First step: In this step, the cylinder is placed on the source of heat. Very quickly the temperature of the working substance (gas) becomes equal to the temperature T1 of the source. In the index diagram, it is represented by the point A [Fig]. Let the pressure and volume in this state are P1 and V1 respectively. Then the gas is allowed to expand isothermally. During the expansion, it takes Q amount of heat from the source. After isothermal expansion, the pressure and volume of the gas become P2 and V2 respectively. In the figure, it is represented by point B. In this case, work done W = Area ABba.
In the index diagram, work is done for the isothermal expansion, W = area ABba.
Second step: In this step, the cylinder is placed on the insulated platform and the confined gas is allowed to expand adiabatically. In the adiabatic expansion, the temperature of the gas by decreasing becomes equal to temperature T2 of the heat sink. After the adiabatic process, the pressure and volume of the gas are respectively P3 and V3 which is represented by the point C in the figure.
In the index diagram, work done by the adiabatic expansion, W2 = area BCcb.
Third step: Now, the cylinder is placed on the heat sink and the gas is compressed isothermally by the piston. As a result, the pressure of the gas increases. In this step, work is done by the piston on the gas. During compression, it rejects Q amount of heat to the sink at temperature T2. The pressure and volume of the gas in this step are P4 and V4 respectively. This is represented by point D in the diagram.
The CD portion of the index diagram represents compression of the gas at temperature T2 and the work done, W3 = area CcdD.
Fourth step: In this step, the cylinder is placed on the insulated platform and the confined gas is allowed to compress adiabatically. Due to the work is done on the confined gas the temperature of the gas increases and becomes equal to the temperature of the source. In this process, the pressure and volume of the gas are P1 and V1 respectively i.e., the cycle returns in its initial state. In the diagram, point A represents this state Graph DA in the index diagram indicates the adiabatic compression and work done in this step, W = area DdaA.
Now according to the convention, work done by the confined gas is positive and work done on this gas is negative. Hence, W1 and W2 are positive and W3 and W4 are negative.
So, total work done by the confined gas is,
W = W1 + W2 – W3 – W4 = area ABCD
From the above discussion, it is evident that in the Carnot’s cycle the work done by this working substance i.e., gas is represented by two isothermal graphs and two adiabatic graphs m the index diagram and are equal to the areas under the graphs. This cycle is called the Carnot’s cycle. In this way, the principles of Carnot’s cycle can be explained in four steps.