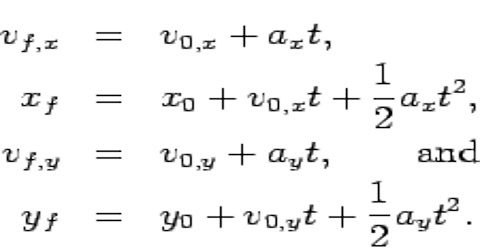First Equation of Dimensional Motion
In one dimensional motion a body moves along a straight line. So quantities associated with motion, for example displacement, velocity, acceleration etc., have only one component (moving along X-axis will have X-component and Y and Z components will be zero). In deriving equations of linear motion we will consider that the body is moving along X-axis. In that case subscripts associated with different quantifies of motion may be omitted. Normally, vx will be represented by v and ax by a.
(i) Equation of position or displacement of a body moving with uniform velocity.
(s = vt) or x = x0 + vxt.
Let an object move with uniform velocity v. The object travels in 1 sec a distance, v x 1. So, in t seconds, it travels the distance, vt.
Let the distance travelled in t sec be, s.
So, S = vt … … … (1)
For one dimensional motion, say along X-axis, if x0 is the position at t = 0 and final position at t = t is x. then s = x – x0.
From equation (1), we get
x – x0 = vxt, here vx is the uniform velocity along X-axis.
or, x = x0 + vxt … … … (ii)
Similarly, for Y and Z-axis, we get,
y = y0 + vyt and z = z0 + zyt
(ii) Relation between displacement, velocity and time of a body moving with variable velocity.
If the body is in motion with variable or non-uniform velocity, then average velocity is taken.
Let at time t = 0, the initial position of the body be x0 and at time t its position be x.
So, displacement of the body, ∆x = x – x0 and elapsed time, ∆t = t – 0 = t.
We know,
average velocity, v = ∆x/∆t = (x – x0)/∆t
or, (x – x0) = vt
or, x = x0 + vt … … … (2)
If the body start from origin, x0 = 0, then equation (2) becomes: x = vt
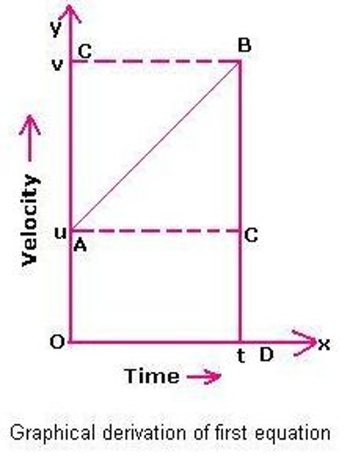
(iii) Relation between displacement, velocity and time of a body moving with uniform acceleration.
Let an object move with uniform acceleration along X-axis. If at time interval ∆t the displacement of the object is ∆x, then average velocity,
v = ∆x/∆t = (x – x0)/t .. … …. (3)
Here at t = 0; at the start, the position of the objects is x0 and at time t, the position is x.
Now, average velocity of an object moving with uniform acceleration is halt of the sum of the initial and final velocities i.e.,
v = (v0 + v)/2; here v0 = initial velocity and v = final velocity.
Putting this value in equation (3), we get;
(v0 + v)/2 = (x – x0)/t
(x – x0) = ½ (v0 + v)t
or, x = x0 + ½ (v0 + v)t … … … (4)
If displacement ∆x = x – x0 = α; then equation (4) can be written as:
S = ½ (v0 + v)t