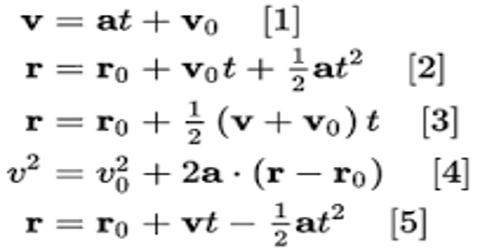Fifth equation
Let the initial velocity of an object moving with uniform acceleration ‘a’ be v0. We need to find the distance traveled by the object at a particular second. Let the distance traveled at t-th second be st. It is equal to the difference between the distances traveled by the object in time t second and (t – 1) second.
st = distance traveled in t sec — distance traveled in (t – 1) sec.
= (v0t + ½ at2) – {v0 (t-1) + ½ a (t-1)2} (from forth equation)
= v0t + ½ at2 – {v0t – v0 + ½ a (t2 – 2t + 1)}
= v0t + ½ at2 – {v0t – v0 + ½ a t2 – at + ½ a)}
= v0t + ½ at2 – v0t + v0 – ½ a t2 + at – ½ a
= v0 + at – ½ a = v0 + ½ a (2t – 1)
so, st = v0 + ½ a (2t – 1) … … … (1)
If the object start from rest, then v0 = 0;
then, st = ½ a (2t – 1)
When the object moves with uniform retardation, equation (1) becomes;
st = v0 – ½ a (2t – 1)