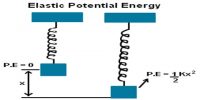
Consider one mole of an ideal gas enclosed in a cylinder with perfectly conducting walls and fitted with a perfectly frictionless and conducting piston. Let P1, V1 and T be the initial pressure, volume and temperature of the gas. Let the gas expand to a volume V2 when pressure reduces to P2, at constant temperature T. At any instant during expansion let the pressure of the gas be P. If A is the area of cross section of the piston, then force F = P x A.
Let assume that the pressure of the gas remains constant during an infinitesimally small outward displacement dx of the piston.
Work done, dW = Fdx = PAcbc = PdV
Total work done by the gas in expansion from initial volume V1 to final volume V2 is
W = v2∫v1 PdV
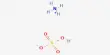
We know, PV = RT, so, P = RV
Then, W = v2∫v1 (RT/V) dV = RT v2∫v1 (1/V) dV
So, W = RT [logeV]v2v1
W = RT [logeV2 – logeV1]
= RT loge (V2/V1)
W = 2.3026 RT log10 (V2/V1)
This is the equation for workdone during an isothermal expansion.