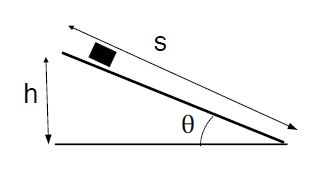
We start from the kinematics equation in one dimension with time eliminated, v2 – v02 = 2aΔx. We multiply by the mass of the object and re-arrange,
(m /2) v2 – (m/2) v02 = ma * Δx = F * Δx ……. ………. (1)
We define the kinetic energy
KE = (m /2) v2 ……. ……. …..(2)
We note that the kinetic energy depends on the magnitude of the velocity, but not the direction of motion; the LHS of 2nd Equation is the change in kinetic energy.
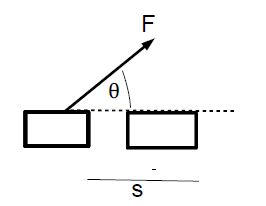
For the RHS we define the work as, W = Fs cosθ. …. ……… (3)
We then find the work-kinetic energy theorem: W = ΔKE = KE — KE0.
The units of work [and the kinetic energy] are: [W] = [KE] = [F] [s] = N • m = J, or Joules.
We consider a few illustrative cases: (1) if a ball is in free fall, the weight mg is the only force acting on the ball. If the ball travels upwards, the work done by the weight is negative, such that the kinetic energy decreases, ΔKE < 0, and the ball slows down. Likewise, if the ball falls downwards, the work done by the weight is positive and the change in kinetic energy is positive, ΔKE < 0, and the ball speeds up. (2) When an object slides across a frictionless horizontal surface [e.g., an ice skater], the forces acting on the skater are the weight and the normal force that are both in a vertical direction. Thus, we have for the angle B = 90°, so that cos θ = 0 and the work done by both forces is zero, W = 0. This implies that the kinetic energy of the object does not change ΔKE < 0, and the speed of the object remains constant.
The normal force is always perpendicular to the surface, while displacement is parallel to the surface. Thus, the angle B between the normal force and the displacement is θ = 90°, and the work is equal to zero W = 0. The normal force is an example of a contstraint force: work done by constraint forces are always zero.
When a person holds a weight and stretches the arms, the arm muscles i obviously do work [felt by fatiguing of the muscles], and yet the mechanical work defined in Equation (3) is zero. This example shows that our intuitive sense of work can sometimes be different from the definition used in physics. The cells in the muscles produce tension by continuously stretching and contracting. Thus, microscopic cell displacements are parallel to the force (tension), so muscle cells do non-zero work.
If a racket hits a tennis ball, the ball will accelerate so that it acquires the speed v starting from rest v0. The force exerted by the racket on the ball is W = mv2/ 2, where m is the mass of the ball. If the tennis ball is distorted by a distance s [much smaller than the radius of the ball], the average force is Fave = W/s . We see that the force becomes larger Fave = ∞ as the distortion becomes smaller s → 0. This shows that there is no such thing as a completely rigid object; even a golf or steel ball is distorted slightly when hit by another object.