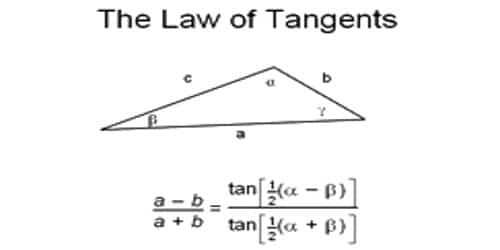
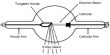
A magnetic needle suspended, at a point where there are two crossed magnetic fields acting at right angles to each other, will come to rest in the direction of the resultant of the two fields. The tangent law of magnetism is a way to contrast the strengths of two magnetic fields that are perpendicular to each other. The law of tangents describes the relationship between the tangent of two angles of a triangle and the lengths of the opposite sides.
B1 and B2 are two uniform magnetic fields acting at right angles to each other. A magnetic needle placed in these two fields will be subjected to two torques tending to rotate the magnet in opposite directions. The torque τ1 due to the two equal and opposite parallel forces mB1 and mB1 tend to set the magnet parallel to B1.
Similarly, the torque τ2 due to the two equal and opposite parallel forces mB2 and mB2 tend to set the magnet parallel to B2. In a position where the torques balance each other, the magnet comes to rest. Now the magnet makes an angle θ with B2 as shown in the Figure.
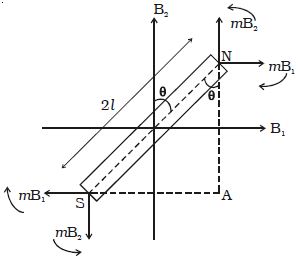
The deflecting torque due to the forces mB1 and mB1
τ1 = mB1 x NA
= mB1 x NS cos θ
= mB1 x 2Ɩ cos θ
= 2Ɩ mB1 cos θ
So, τ1 = MB1 cos θ
Similarly the restoring torque due to the forces mB2 and mB2
τ2 = mB2 x SA
= mB2 x 2Ɩ sin θ
= 2Ɩ m x B2 sin θ
so, τ2 = MB2 sin θ
At equilibrium, τ1 = τ2
MB1 cos θ = MB2 sin θ
so, B1 = B2 tan θ
This is called Tangent law
Invariably, in the applications of tangent law, the restoring magnetic field B2 is the horizontal component of Earth’s magnetic field Bh. If a compass or other magnet is subjected to a magnetic field B that is perpendicular to the horizontal magnetic field of the Earth (Bh), it will rest at an angle theta to the Earth’s magnetic field. The relationship between the two magnetic fields is:
B = Bh(tan theta).
Because the tangent of the angle is the relevant factor here, the law is called the tangent law of magnetism. It represents the relationship between the tangent of two angles of a triangle and the length of the opposite sides.
To understand the law of tangents in an enhanced way, we will need three pieces of information for a common triangle even it may or may not be a triangle. The four cases involved are:
- Two sides and one opposite angle.
- One side and two angles.
- Three Sides.
- Two sides and the angle between them.