The equation P = – ΔW/ΔV can be interpreted as the work necessary to “create” volume. Likewise, work is necessary to create surface area ΔA, and we define
σ = – (ΔW/ΔA)
The quantity σ is referred to as surface tension with unit [σ = J/m2 = N/m]. Alternatively, pressure is the force divided by area P = F/A and the surface tension is equal to force divided by length σ = F/L.
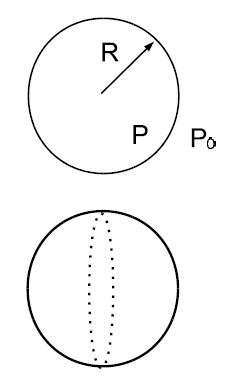
We consider a droplet of radius R. The pressure inside the droplet is P, while the pressure outside is P0 [e.g., atmospheric pressure]. We assume that the droplet is in mechanical equilibrium so that it neither grows or shrinks. We cut the droplets into two hemispherical shells: the pressure difference produces the force (P — P0) • πR2. This outward force is balanced by the force produced by the surface tension σ • 2πR . We set the two forces equal to each other, and find
P — P0 = σ/2R
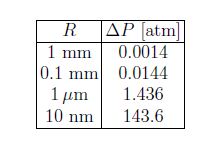
This is called Laplace law. The pressure difference thus increases with decreasing size of the droplet. For water droplets:
We consider two small droplets with radii R1 and R2 < R1, respectively: the total energy can be reduced if the small droplet shrinks and the larger droplet grows. This mechanism is responsible for the formation of large rain drops in the atmosphere.