We consider a wheel with radius r that rolls without slipping. This means that the distance d is equal to arc-length s = rθ,
d = rθ ….. …… (1)
If the center of the wheel travels the distance d in the time t, we have for the linear speed v = d/t , and for the angular speed to ω = θ/t . We find v = (rθ)/t = r(θ/t) or
Vt = rω …. …. (2)
Similarly, if the center of the wheel accelerates from v0 = 0 to the velocity v in time t, the angular velocity increases from ω0 to ω . Since v = rω , we find
At = rα … …… (3)
Here, v and a are the velocity and acceleration of a point on the perimeter relative to the the center: i.e., they are the tangential velocity and acceleration, vT = ωr and aT = αr.
Example: a) A car travels at the speed v = 25 m/s. Find the angular speed of the wheels when the radius of the wheel is r = 0.31 m (1 foot). b) If the car accelerates from rest to v = 25 mis in the time t = 17s, find the angular acceleration of the wheel, and the number of turns of the wheeL
Solution: We find for the angular speed,
ω = v/t = 25m / s = 80.6 (rad/s)
We find for the angular acceleration,
α = (ω – ω0)/t = (80.6 (rad/s) – 0) / 17s = 4.74 (rad/s2)
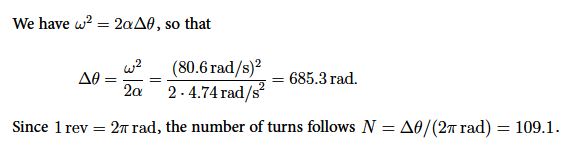
The speed is constant for uniform circular motion speed. Since the angular acceleration is zero α = 0, and the tangential acceleration is zero as well. Since v = ωr, we find for the centriptal acceleration towards the center, ac = v2t/r or,
Ac = vω2.
For rolling motion of a wheel without slipping, the linear speed of the center must be the same as tangential speed: vCM = rω.