A force can rotate a nut when applied by a wrench or it can open a door while the door rotates on its hinges; in addition to the tendency to move a body in the direction of the application of a force, a force also tends to rotate the body about any axis which does not intersect the line of action of the force and also not parallel to it. This tendency of rotation is called turning effect of a force or moment of the force about the given axis.
The magnitude of the moment of force F about a point is defined as the product of the magnitude of force and the perpendicular distance of the point from the line of action of the force.
Let consider a force F acting at the point P on the body as shown in Figure. Then, the moment of the force F about the point 0 = Magnitude of the force x perpendicular distance between the direction of the force and the point about which moment is to be determined =F x OA.
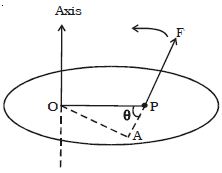
If the force acting on a body rotates the body in anticlockwise direction with respect to O then the moment is called anticlockwise moment. On the other hand, if the force rotates the body in clockwise direction then the moment is said to be clockwise moment. The unit of moment of the force is N m and its dimensional formula is ML2 T-2.
As a matter of convention, an anticlockwise moment is taken as positive and a clockwise moment as negative. While adding moments, the direction of each moment should be taken into account.
In terms of vector product, the moment of a force is expressed as, m = r x F.
Where r is the position vector with respect to O. The direction of m is perpendicular to the plane containing r and F.