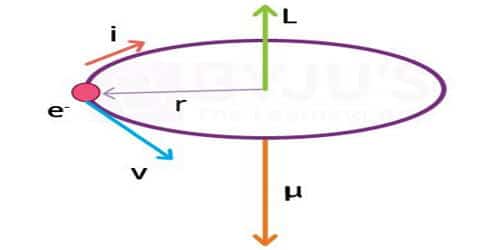
The magnetic dipole moment of a revolving electron
According to Neil Bohr’s atom model, the negatively charged electron is revolving around a positively charged nucleus in a circular orbit of radius r. The revolving electron in a closed path constitutes an electric current. The motion of the electron in the anticlockwise direction produces a conventional current in the clockwise direction.
Current, i = e/T; where T is the period of revolution of the electron.
If v is the orbital velocity of the electron, then
T = 2πr/v
so, i = ev/2πr
Due to the orbital motion of the electron, there will be orbital magnetic moment μl
μl = i A, where A is the area of the orbit
μl = ev/2πr . πr2
μl = evr/2
If m is the mass of the electron
μl = e/2m (mvr)
mvr is the angular momentum (l) of the electron about the central nucleus.
μl = e/2m.l … … (1)
μ/l = e/2m; is called gyromagnetic ratio and is a constant. Its value is 8.8 × 1010 C kg-1. Bohr hypothesized that the angular momentum has an only discrete set of values given by the equation.
l = nh/2π … … (2) where n is a natural number and h is the Planck’s constant = 6.626 × 10-34 Js.
Substituting equation (2) in equation (1)
μl = e/2m . nh/2π = neh/4πm
The minimum value of the magnetic moment is
(μl)min = eh/4πm, n = 1
The value of eh/4πm is called Bohr magneton
By substituting the values of e, h, and m, the value of Bohr magneton is found to be 9.27 × 10-24 Am2.
The Bohr Magneton is used very widely to express magnetic moments at the atomic scale. In addition to the magnetic moment due to its orbital motion, the electron possesses a magnetic moment due to its spin. Hence the resultant magnetic moment of an electron is the vector sum of its orbital magnetic moment and its spin magnetic moment. The expression we obtained is good for only simple atoms like hydrogen and does not predict all the magnetic moment states of an electron.
The spin and orbital magnetic moments of atoms combine vectorially in a sample to produce the net magnetic moment of that particular sample. The electron does not really revolve around the nucleus. Instead, the electron’s orbital magnetic moment is obtained by virtue of being trapped in the nuclei (plural of nucleus) potential well. It is these magnetic moments obtained by the combination of orbital and spin magnetic moments determine the magnetic properties of the materials.