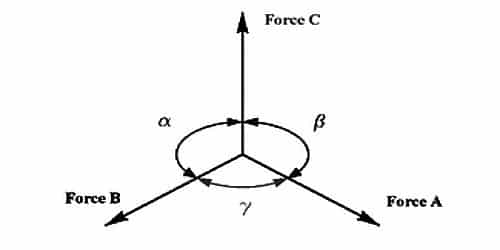
Lami’s theorem states that if three forces acting at a point are in equilibrium, then each of the force is directly proportional to the sine of the angle between the remaining two forces. It gives the conditions of equilibrium for three forces acting at a point.
Lami’s theorem states that if three forces stand-in at a position is in symmetry, each force is comparative to the sine of the angle between the other two forces. The angle between the force vectors is taken when all the three vectors are emerging from the particle.
Let consider three forces P, Q, and R acting at a point O (figure). Under the action of three forces, the point O is at rest, then by Lami’s theorem,
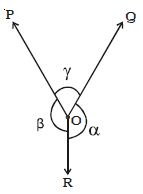
P ∞ Sin α
Q ∞ Sin β
And R ∞ Sin ϒ then,
[P/Sin α] = [Q/Sin β] = [R/Sin ϒ] = Constant.
Three coplanar forces acting at a point will be in symmetry if each force is proportional to the sine of the angle between the other two.