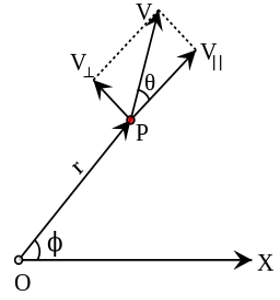
The rate of change of angular displacement is called the angular velocity of the particle.
Let dθ be the angular displacement made by the particle in time dt, then the angular velocity of the particle is ω = dθ/dt. Its unit is rad s-1 and the dimensional formula is T-1.
For one complete revolution, the angle swept by the radius vector is 360° or 2π radians. If T is the time taken for one complete revolution, known as period, then the angular velocity of the particle is: ω = θ/t = 2π/t.
If the particle makes n revolutions per second, then, ω = 2π (1/T) = 2π n where n = 1/T is the frequency of revolution.