Demonstration of Interference of Sound: The phenomenon of interference between two longitudinal waves in air can be demonstrated by Quincke’s tube shown in Figure.
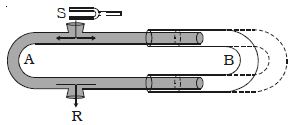
Quincke’s tube consists of U shaped glass tubes A and B. The tube SAR has two openings at S and R The other tube B can slide over the tube A. A sound wave from S travels along both the paths SAR and SBR in opposite directions and meet at R.
If the path difference between the two waves (i.e) SAR ≈ SBR is an integral multiple of wavelength, intensity of sound will be maximum due to constructive interference.
SAR ≈ SBR = nλ
The corresponding phase difference Φ between the two waves is even multiples of π.
Φ = m 2π where m = 0, 1, 2, 3 ….
If the tube B is gradually slided over A. a stage is reached when the intensity of sound is zero at R due to destructive interference. Then no sound will be heard at R.
If the path difference between the waves is odd multiples of λ/2 intensity of sound will be minimum.
SAR ≈ SBR = (2m + 1) λ/2
The corresponding phase difference Φ between the two waves is odd multiples of π.
So, Φ = (2m + 1) π where m = 0, 1, 2, 3… …