Total Internal Reflection by Wave Theory:
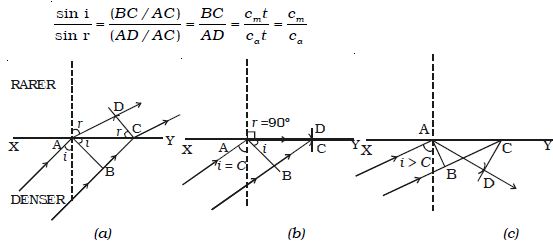
Let XY be a plane surface which separates a rarer medium (air) and a denser medium. Let the velocity of the wavefront in these media be Ca and Cm respectively.
A plane wavefront AB passes from denser medium to rarer medium. It is incident on the surface with angle of incidence i. Let r be the angle of refraction.
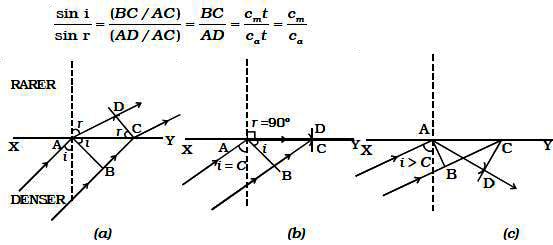
Fig: Total internal reflection
Since Cm/Ca < 1 , i is less than r. This means that the refracted wavefront is deflected away from the surface XY.
In right angled triangle ADC, there are three possibilities
(i) AD < AC (ii) AD = AC and (iii) AD > AC
(i) AD < AC : For small values of i, BC will be small and so
AD > BC but less than AC (Fig. a)
sin r = AD/AC, which is less than unity
i.e r < 900
For each value of i, for which r < 900, a refracted wavefront is possible
(ii) AD = AC : As i increases r also increases. When AD = AC,
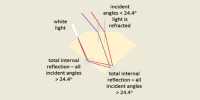
sin r = 1 (or) r = 900. i.e a refracted wavefront is just possible (Fig. b). Now the refracted ray grazes the surface of separation of the two media. The angle of incidence at which the angle of refraction is 900 is called the critical angle C.
(iii) AD > AC : When AD > AC, sin r > 1. This is not possible (Fig: c). Therefore no refracted wave front is possible, when the angle of incidence increases beyond the critical angle. The incident wavefront is totally reflected into the denser medium itself. This is called total internal reflection.
Hence for total internal reflection to take place (i) light must travel from a denser medium to a rarer medium and (ii) the angle of incidence inside the denser medium must be greater than the critical angle. i.e i > C.