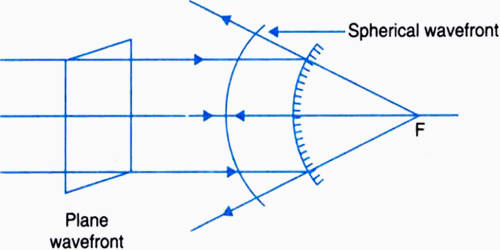
Refraction of a plane wavefront at a plane surface
Let XY be a plane refracting surface separating two media 1 and 2 of refractive indices μ1 and μ2 (Figure). The velocities of light in these two media are respectively c1 and c2. Consider a plane wavefront AB incident on the refracting surface at A. PA and QBC are perpendiculars drawn to AB at A and B respectively. Hence they represent incident rays. NAN1 is the normal drawn to the surface. The wavefront and the surface are perpendicular to the plane of the paper.
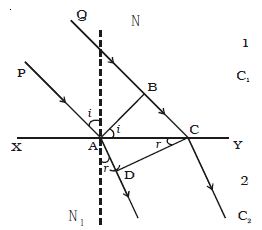
Fig: Refraction of a plane wavefront at the plane surface.
At any instant, the resultant displacement of a particle in the medium depends on the phase difference between the waves and is the algebraic sum of the displacement it would have at the same instant due to each separate set.
Refraction using Huygen’s principle
We know that when light travels from one transparent medium to another transparent medium its path changes. So the laws of refraction state that the angle of incidence is the angle between the incident ray and the normal and the angle of refraction is the angle between the refracted ray and the normal. According to Huygen’s principle each point on the wavefront act as the source of secondary wavelet. By the time, the secondary wavelets from B, reaches C, the secondary wavelets from the point A would travel a distance AD = C2t, where t is the time taken by the wavelets to travel the distance BC.
∴ BC = C1t and AD = C2t = C2 BC/C1.
Taking A as a centre and C2 BC/C1 as radius an arc is drawn in the second medium. From C a tangent CD is drawn to this arc. This tangent CD not only envelopes the wavelets from C and A but also the wavelets from all the points between C and A. Therefore CD is the refracted plane wavefront and AD is the refracted ray.
The incident ray, reflected ray and the normal, to the interface of any two given mediums all lie in the same plane. We also know that the ratio of the sine of the angle of incidence and sine of the angle of refraction is constant.