Reflection of a plane wave front at a plane surface
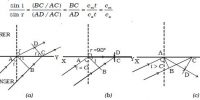
Let XY be a plane reflecting surface and AB be a plane wavefront incident on the surface at A. PA and QBC are perpendiculars drawn to AB at A and B respectively. Hence they represent incident rays. AN is the normal drawn to the surface. The wave front and the surface are perpendicular to the plane of the paper (Figure).
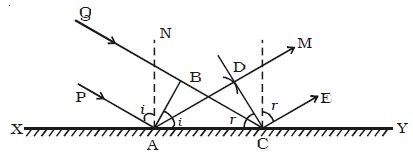
Fig: Reflection of a plane wavefront at a plane surface.
According to Huygen’s principle each point on the wavefront acts as the source of secondary wavelet. By the time, the secondary wavelets from B travel a distance BC, the secondary wavelets from A on the reflecting surface would travel the same distance BC after reflection.
Taking A as centre and BC as radius an arc is drawn. From C a tangent CD is drawn to this arc. This tangent CD not only envelopes the wavelets from C and A but also the wavelets from all the points between C and A. Therefore CD is the reflected plane wavefront and AD is the reflected ray.
Laws of reflection
(i) The incident wavefront AB, the reflected wavefront CD and the reflecting surface XY all lie in the same plane.
(ii) Angle of incidence i = ∠ PAN = 900 − ∠ NAB = ∠BAC
Angle of reflection r = ∠ NAD = 900 − ∠ DAC = ∠DCA
In right angled triangles ABC and ADC
∠B = ∠ D = 900
BC = AD and AC is common
∴ The two triangles are congruent
∠ BAC = ∠DCA
i.e. i = r
Thus the angle of incidence is equal to angle of reflection.