Magnetic Induction along the axis of Circular Coil Carrying Current:
Let consider a circular coil of radius ‘a’ with a current I as shown in Figure. P is a point along the axis of the coil at a distance x from the centre O of the coil.
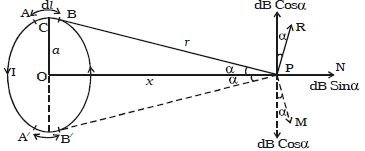
AB is an infinitesimally small element of length dl. C is the midpoint of AB and CP = r
According to Biot– Savart law, the magnetic induction at P due to the element dl is
dB = μ/4π (Idl sinθ)/r2; where θ is the angle between Idl and r
Here, θ = 900
dB = μ/4π [Idl/r2]
The direction of dB is perpendicular to the current element Idl and CP. It is therefore along PR perpendicular to CP.
Considering the diametrically opposite element A′B′, the magnitude of dB at P due to this element is the same as that for AB but its direction is along PM. Let the angle between the axis of the coil and the line joining the element (dl) and the point (P) be α. dB is resolved into two components:- dB sin α along OP and dB cos α perpendicular to OP. dB cos α components due to two opposite elements cancel each other whereas dB sin α components get added up. So, the total magnetic induction at P due to the entire coil is
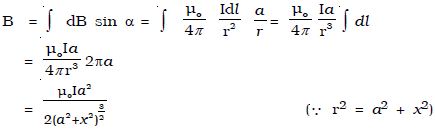
If the coil contains n turns, the magnetic induction is
B = [μ0 nIa2] / 2(a2+x2)3/2
At the centre of the coil, x = 0
B = μ0 nI/2a