Let consider a conductor PQ of length l and area of cross section A.
The conductor is placed in a uniform magnetic field of induction B making an angle θ with the field [Figure]. A current I flows along PQ. Hence, the electrons are drifted along QP with drift velocity vd. If n is the number of free electrons per unit volume in the conductor, then the current is
I = nAvde
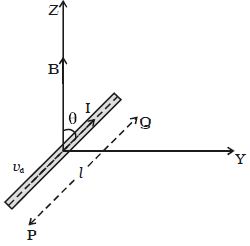
Fig: Force on a current carrying conductor placed in a magnetic field
Multiplying both sides by the length l of the conductor,
∴ Il = nAvdel.
Therefore the current element,
→Il = →-nAvdel … (1)
The negative sign in the equation indicates that the direction of current is opposite to the direction of drift velocity of the electrons.
Since the electrons move under the influence of magnetic field, the magnetic lorentz force on a moving electron.
→f = –e (→vd × →B) … (2)
The negative sign indicates that the charge of the electron is negative.
The number of free electrons in the conductor
N = nAl … (3)
The magnetic lorentz force on all the moving free electrons
→F = →Nf
Substituting equations (2) and (3) in the above equation
→F = nAl { –e (→vd × →B)}
→F = –nAl e →vd × →B … (4)
Substituting equation (1) in equation (4)
→F = Il × →B
This total force on all the moving free electrons is the force on the current carrying conductor placed in the magnetic field.