Name of the Experiment: Comparing the Masses with the help of Spring
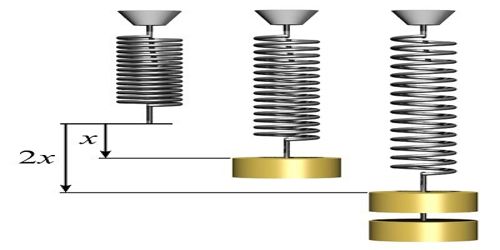
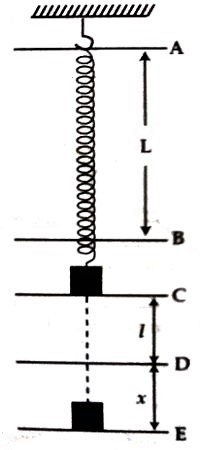
Theory: If a mass ‘m’ of a body is hanged at the end of a spiral spring hanged vertically. The length of the spring increases by ‘l’. In this condition the spring is considered to be in equilibrium. Now, if the body is pulled downward by ‘A’ distance ‘x’ and is released. Then it oscillates with simple harmonic motion [Figure]. If the body is pulled downward a restoring force acts on the spring along its initial position. According to Hooke’s law displacement force ‘x’ is proportional to the restoring force and oppositely directed. So F = – K’x; here Kꞌ is the force constant of the sprung.
When the body is released after pulling it, the body moves with acceleration a due to the force F. If the mass of the, body is m, then its acceleration will be
a = F/m
then, a = (-Kꞌ/m)x
so, a = Kx, here K = Kꞌ/m
Since for unit displacement, acceleration of the body is Kꞌ/m; so time period of the oscillating body is-
T = 2π √(m/K)
or, T2 = 4π2 (m/K)
so, m = T2K/4π2 … … … (1)
If the masses of two bodies are m1 and m2 and time period for these two mass are T1 and T2 respectively, then from (1) it can be written as-
m1 = T12K/4π2
and, m2 = T22K/4π2
So, m1/ m2 = (T12K/4π2) x (4π2/ T22K)
then, m1 : m2 = T12 : T22
Equipments:
(1) A spring of known spring constant.
(2) A hook to hang the spring.
(3) Bodies of different masses.
(4) Stop watch.
(5) An wooden meter scale.
Procedure:
(1) The spring is to be hanged by a hook from rigid body. If the experimented first body of mass m1 is hanged from the lower end of the spring; then length will increase and at a particular position will be stable. It is the equilibrium point.
(2) Mark on the wall or on a long scale, to maintain the correct position of the equilibrium point.
(3) Then if by pulling the body slightly from the equilibrium position and the released, the spring will oscillate up and down. In this condition, record time for 20 oscillations and repeat this process three times. Each time divide the time by the number of oscillation and determine Time, period (T1). Take average T1 from the value of three readings.
(4) Following the similar procedure 3 record time period T2 for the second mass m2.