Determination of current and potential difference by using Kirchoff’s laws and the establishment of the Wheatstone bridge principle.
Kirchoff’s Law states that the algebraic sum of currents at a junction of an electric circuit is zero.
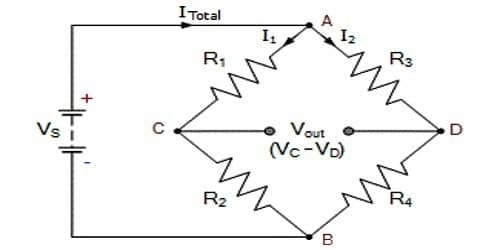
If four junctions are made due to the formation of a closed-loop by connecting four resistors in series and if an electric cell is connected between the two opposite junctions and a galvanometer is connected between the other two opposite junctions then the circuit thus formed is called Wheatstone bridge. The Wheatstone bridge is a circuit which is used to measure correctly an unknown resistance.
Wheatstone bridge principle states that when the bridge is impartial, the products of the resistance of the opposite arms are equivalent.
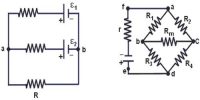
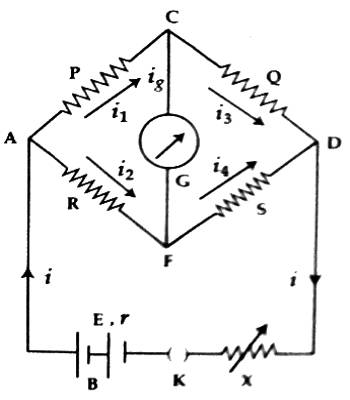
Let us consider that four resistors P, Q, R, and S are arranged like tetrahedral ACDF. Wheatstone bridge is formed by connecting a battery B or an electric source, a plug key K and a variable resistor X between the junctions A and D and a galvanometer G between the junctions C and D [Figure].
Compared to the other measuring instruments such as voltage divider, the perception of the Wheatstone bridge is broadly used because of the accurateness in its measurement of resistance.
Components of Wheatstone bridge experimentation –
- A resistor with an unknown resistance value,
- Two resistors (with known resistance value),
- Variable Resistor,
- Voltage/DC source,
- Galvanometer and
- Connecting Wires.
Let the resistance of the galvanometer be G and currents flowing through P, Q, S, and G be respectively i1, i2, i3, i4, and ig.
Now, applying Kirchhoff’s first law respectively at points C and F. we get,
i1 – i3 – ig = 0 i.e., i1 = i3 + ig … … … (1)
and, i2 + ig – i4 = 0 i.e., i4 = i2 + ig … … … (2)
Again, applying Kirchhoff’s second law respectively at closed loops ACFA and CDFC, we get,
i1P + igG – i2R = 0 … … … (3)
and, i3Q – i4S – igG = 0 … … … (4)
But at balanced condition of the bridge, ig = 0.
So, under this condition, according to equations (1) and (2), i1 = i3 and i4 = i2.
According to equations, (3) and (4), i1P = i2R … … … (5)
and i3Q = i4S … … … (6)
Now dividing equation (5) by equation (6) we get
i1P / i3Q = i2R / i4S; but, i1 = i3 and i4 = i2
So, P / Q = R /S … … … (7)
According to the equation (7), at the equilibrium of the Wheatstone bridge, if values of any three resistors are known, then the resistance of the fourth resistor can be determined. It is called the Wheatstone bridge principle for the measurement of resistance.
Condition for zero deflection of the galvanometer –
(i) The potential difference between two terminals of the galvanometer will be zero, i.e., no current will flow through the galvanometer. Under this condition,
(VA – VD) = (P + Q)i1 = (R + S)i2
(ii) The ratio of the two resistances in the same order on both sides of the galvanometer will be equal.
i.e., P/Q = R/S.
[N.B. In the figure, arms AC, CD, AF, and FD) are called first, second, third, and fourth arm of the Wheatstone bridge. In the Balanced Bridge situation, the current through the galvanometer is zero and also the voltage dissimilarity between the points becomes zero, i.e., at both points voltage level would be similar.]