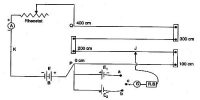
Whenever current flows through a coil, the self−inductance opposes the growth of the current. Hence, some work has to be done by external agencies in establishing the current. If e is the induced emf then,
e = – L (dI/dt)
The small amount of work dw done in a time interval dt is
dw = e.I dt
= −L (dI/dt) I.dt
The total work done when the current increases from 0 to maximum value (I0) is
w= ∫dw= l∫0 −L I dI
This work done is stored as magnetic potential energy in the coil.
∴ Energy stored in the coil
= −L l∫0 IdI = – ½ . L I02
Negative sign is consequence of Lenz’s Law. Hence, quantitatively, the energy stored in an inductor is: ½.L I02