Divergence
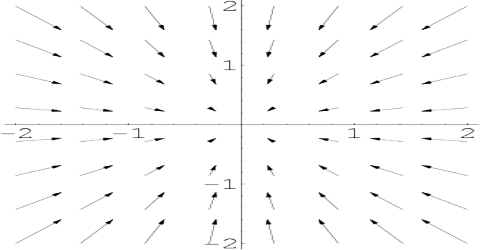
The divergence is an operator, which takes in the vector-valued function defining this vector field, and outputs a scalar-valued function measuring the change in density of the fluid at each point. Let in three-dimensional space, the position vector of a vector field of the region R be,
V→ (x, y, z) = v1 (x, y, z) î + v2 (x, y, z) ĵ + v3 (x, y, z) ƙ; then the scalar product of V→ with the operator ∆ is called divergence of that vector field.
Divergence is expressed as, ∆→ V→ or div.V→. Mathematically it can be written as;
∆→ V→ = [(∂/∂x) î + (∂/∂y) ĵ + (∂/∂z) ƙ] . (v1 î + v2 ĵ + v3 ƙ)
= ∂v1/∂x + ∂v2/∂y + ∂v3/∂z; it is a scalar quantity.
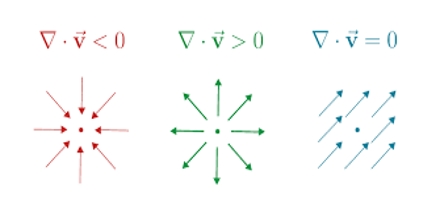
Physical properties of divergence
(i) Divergence expresses the total amount of flux of a vector quantity that converges towards and diverges from a point. Divergence expresses the amount of flux. By ∆→.V→ or div.V→ it is meant change of density of a fluid in unit time.
(ii) If the value is positive, then value of the fluid increases density decreases.
(iii) If the value is negative, the volume shrinks, density increases,
(iv) If the value is zero, then incoming and outgoing flux becomes equal.
(v) If the divergence of a quantity becomes zero, i.e., . V = 0, then that vector held is called solenoid.