Differential Equation of the simple harmonic motion
Simple harmonic motion is produced due to the oscillation of a spring. Find out the differential equation for this simple harmonic motion. Suppose mass of a particle executing simple harmonic motion is ‘m’ and if at any moment its displacement and acceleration are respectively x and a, then according to definition,
a = – (K/m) x, K is the force constant.
But a = d2x/dt2
So, d2x/dt2 = – (K/m) x … … … (1)
In order to solve any differential equation, a general procedure is to assume a solution and it is observed whether the given differential equation can be derived from it or not. Suppose the solution of the equation (1) is –
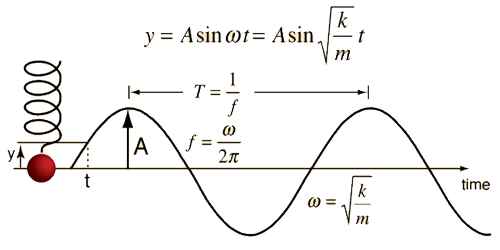
x(t) = a sin ωt, here a and ω are constants.
dx/dt = a ω cos ωt and d2x/dt2 = – a ω2 sin ωt
From equation we get,
– a ω2 sin ωt = – (K/m) a sin ωt
So, if the value of the constant is, ω = √(K/m) … … … (2)
then, the relation x (t) = a sin ωt satisfies the differential equation.
So, a solution of the equation is x(t) = a sin ωt.
Similarly, we can prove that the relation, x(t) = b cos ωt is also a solution. Hence, x(t) = a sin ωt or, x(t) = b cos ωt is the solution of the simple harmonic motion.
It can be proved that,
x(t) = a sin ωt + b cos ωt … … … (3)
This equation is the general solution of the differential equation (1), as,
dx/dt = a ω cos ωt – b ω sin ωt
or, d2x/dt2 = – a ω2 sin ωt – b ω2 cos ωt
= – ω2 (a sin ωt + b cos ωt) = – ω2x
Then, d2x/dt2 = – ω2x (here = a sin ωt + b cos ωt)
So, d2x/dt2 + ω2x = 0 … … … (4)
So, equation (4) is the differential equation of the simple harmonic motion.