An important application of Kirchoff’s law is the Wheatstone’s bridge (Figure).
Wheatstone’s network consists of resistances P, Q, R and S connected to form a closed path. A cell of emf E is connected between points A and C. The current I from the cell is divided into I1, I2, I3 and I4 across the four branches. The current through the galvanometer is Ig. The resistance of galvanometer is G.
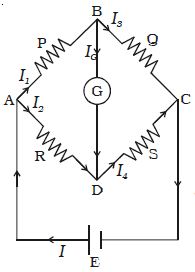
Fig: Wheatstone’s bridge
Applying Kirchoff’s current law to junction B,
I1 – Ig – I3 = 0 … (1)
Applying Kirchoff’s current law to junction D
I2 + Ig – I4 = 0 … (2)
Applying Kirchoff’s voltage law to closed path ABDA
I1 P + Ig G – I2 R = 0 … (3)
Applying Kirchoff’s voltage law to closed path ABCDA
I1 P + I3 Q – I4 S – I2 R = 0 … (4)
When the galvanometer shows zero deflection, the points B and D are at same potential and Ig = 0. Substituting Ig = 0 in equation (1), (2) and (3)
I1 = I3 … (5)
I2 = I4 … (6)
I1 P = I2 R … (7)
Substituting the values of (5) and (6) in equation (4)
I1 P + I1 Q – I2 S – I2 R = 0
I1 (P + Q) = I2 (R+S) … (8)
Dividing (8) by (7)
I1 (P + Q) / I1 P = I2 (R+S) / I2 R
(P + Q) / P = I (R+S) / R
1 + Q/P = 1 + S/R
so, Q/P = S/R or, P/Q = R/S
This is the condition for bridge balance. If P, Q and R are known, the resistance S can be calculated.