Since self-inductance is related to the magnetic field produced by a current, any configuration of conductors possesses self-inductance. Inductance is attained by a coil due to the self-induced emf produced in the coil itself by changing the current flowing through it. This property of inductor or coil due to which it opposes a change of current through it called the inductance denoted by letter L. Unit of inductance is henry (H).
Self Inductance of a Long Solenoid Explanation –
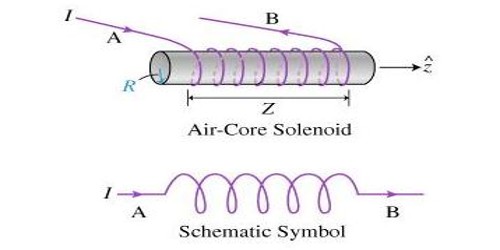
Let consider a solenoid of N turns with length ‘l’ and area of cross-section ‘A’. It carries a current ‘I’. If ‘B’ is the magnetic field at any point inside the solenoid, then,
Magnetic flux per turn = B × area of each turn
But, B = μ0NI / l
Magnetic flux per turn = μ0NIA / l
Hence, the total magnetic flux (φ) linked with the solenoid is given by the product of flux through each turn and the total number of turns. Like a capacitor, an inductor is another component commonly in electronic circuits. [Number of field lines passing through either a real or a fictitious plane in a magnetic field is called magnetic flux.]
φ = (μ0NIA / l) × N
i.e φ = (μ0N2IA / l) … … (1)
If L is the coefficient of self-induction of the solenoid, then
φ = LI … … (2)
From equations (1) and (2)
LI = (μ0N2IA / l)
∴ L = (μ0N2A / l)
If the core is filled with a magnetic material of permeability μ, then, L = (μN2A / l)
A Problem Explanation: A long solenoid with 15 turns per cm has a small loop of area 2.0 placed inside the solenoid normal to its axis. If the current carried by the solenoid changes steadily from 2.0 A to 4.0A in 0.1 s, what is the induced emf in the loop while the current is changing?
Answer
Number of turns on the solenoid = 15 turns/cm = 1500 turns/m
Number of turns per unit length, n = 1500 turns
The solenoid has a small loop of the area, A = 2.0 cm2 = 2 × 10-4m2
Current carried by the solenoid changes from 2 A to 4 A.
Therefore change in current in the solenoid, di = 4 – 2 = 2 A
Change in time, dt = 0.1 s
Induced emf in the solenoid is given by Faraday’s law as:
e = (dΦ/dt) … … … (i)
Where, Φ= Induced flux through the small loop
= BA … … … (ii) [Where B = Magnetic field]
= (μ0ni) … … …(iii)
μ0 = Permeability of free space
=4nx10-7H/m
Hence, equation (i) reduces to:
e = (d/dt) (di/dt)
= Aμ0n x (di/dt)
= 2×10-4x4x3.14×10-7x 1500 x (2/0.1)
= 7.54 x 10-6V
Hence, the induced voltage in the loop is 7.54×10-6V