Let consider an object OO’ on the principal axis of a concave mirror beyond C. The incident and the reflected rays are shown in the Figure. A ray O’A parallel to principal axis is incident on the concave mirror at A, close to P. After reflections the ray passes through the focus F. Another ray O’C passing through centre of curvature C, falls normally on the mirror and reflected back along the same path. A third ray O’P incident at the pole P is reflected along PI’. The three reflected rays intersect at the point I’. Draw perpendicular I’I to the principal axis. II’ is the real, inverted image of the object OO’.
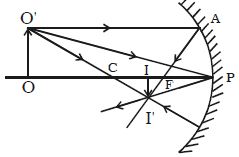
Right angled triangles, II’P and OO’P are similar.
II’/OO’ = PI/PO … … … (1)
Right angled triangles II’F and APF are also similar (A is close to P; hence AP is a vertical line)
so, II’/AP = IF/PF
AP = OO’. Therefore the above equation becomes;
II’/OO’ = IF/PF … … … (2)
Comparing the equation (1) and (2)
PI/PO = IF/PF
but, IF = PI – PF
Therefore the equation become, PI/PO = (PI – PF)/PF
Using sign conventions, we have, PO = – u, PI = – v and PF = – f
Substituting the value in the above equation, we get,
(-v/-u) = {-v-(-f)}/(-f)
or, v/u = (v-f)/f = v/f – 1
Dividing the v and rearranging, 1/u + 1/v = 1/f
This is called mirror equation.